Simulation of Cavitating Flow in Confined Geometries

Cavitating flows occur in a wide variety of engineering systems. In energy, aerospace, MedTech, and other industrial applications, uncontrolled cavitation can lead to erosion, vibration, efficiency loss, and equipment failure. In pharmaceutical and medical applications, cavitation is deliberately used for processes such as ultrasonic cleaning and drug delivery, yet its highly unsteady and complex behavior remains difficult to predict and control.

Cavitation often occurs when liquid passes through a locally narrowed or confined geometry. As the flow accelerates, the local liquid pressure can drop below the vapor pressure, triggering the formation of dynamic vapor cavities that evolve across a wide range of time and length scales. Accurately predicting and controlling these cavities is critical for guiding the development of products that either incorporate or are susceptible to cavitation.

In this example, we simulate the development of unsteady vapor cavities in cavitating flow over a wedge (Figure 1). The flow exhibits strong periodic cavitation events, producing highly turbulent flow dynamics with inherent multiphase and multiscale interactions. These complexities pose significant computational challenges. 

 

To address the complexities of simulating cavitation in this example of flow over a wedge, the computational fluid dynamics (CFD) experts at Veryst applied non-equilibrium phase-transforming theory and continuum mechanics with a variational multiscale approach, offering a balanced compromise between accuracy, robustness, and efficiency.

Cavitating flow over a wedge is characterized by two dimensionless numbers: the freestream Reynolds and Cavitation numbers. The Reynolds number quantifies the degree of turbulence in the flow, the cavitation number quantifies the likelihood of vapor formation, and “freestream” indicates the portion of the flow away from cavitation. The freestream Reynolds number is defined by

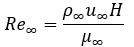
where p_∞, u_∞ and µ_∞ are the freestream density, velocity and viscosity, respectively, and H is the height of the wedge. The freestream cavitation number is defined by

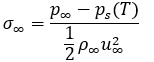
where p_s(T) is the saturation pressure at temperature T and p_∞  is the freestream pressure. In this study, the freestream Reynolds number is 200,000, indicating a highly turbulent flow, and the freestream cavitation number is 1, indicating a strong tendency for cavitation to occur.

 

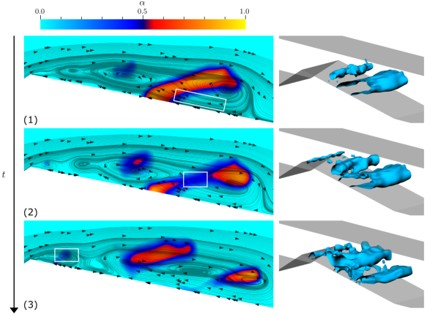
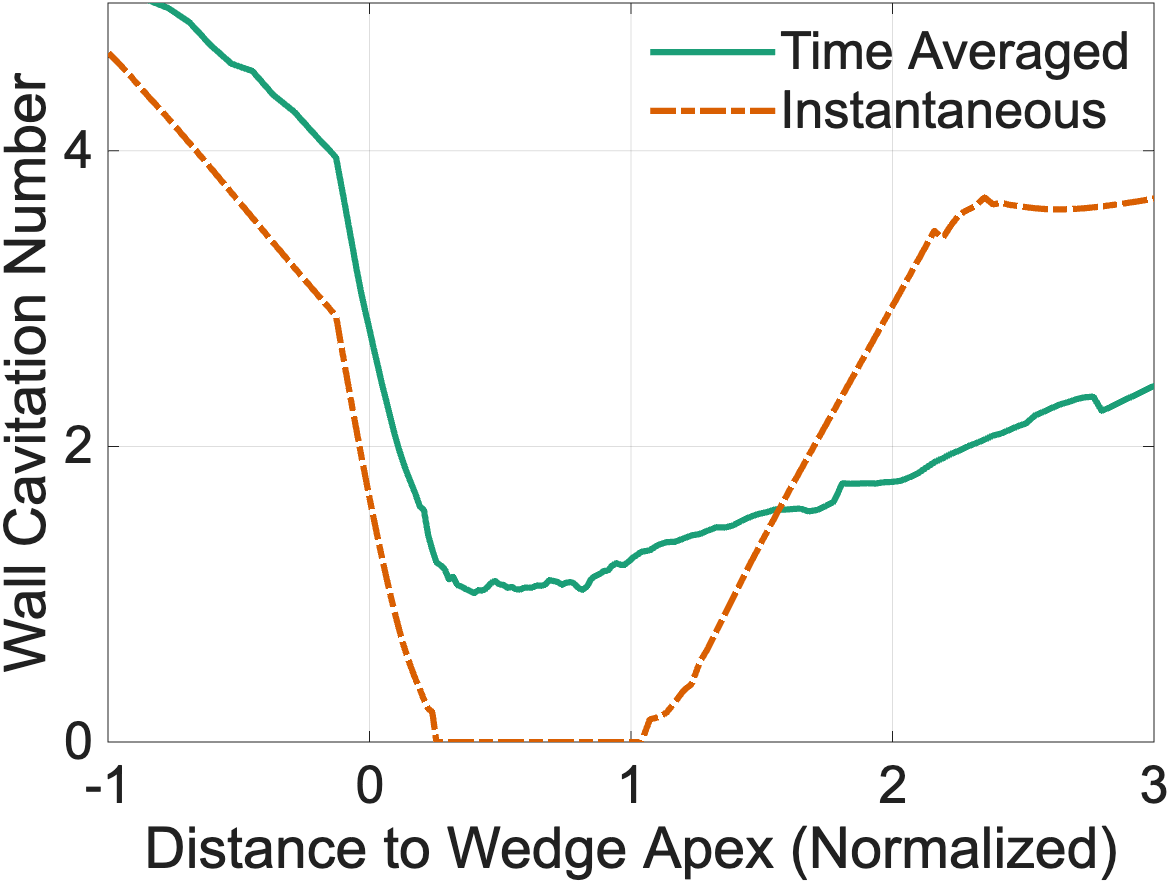
Developing products and processes involving fluid flows that may exhibit or generate cavitation requires understanding both the detailed flow fluctuations and overall pressure and vapor fraction distributions. While Figure 2 shows the instantaneous evolution of a complete cavitation inception–collapse cycle, the time-averaged data in Figure 3 quantifies where cavitation occurs most frequently. Taken together, these perspectives can provide guidance on improving product and process design to avoid cavitation, or to better control cavitation when desired.

 

Our simulation captures the full unsteady evolution of cavitation, as illustrated in Figure 2. As the main vapor sheet grows and moves downstream, pressure forces drive the formation of jets that eventually break the sheet into large vapor clouds. These clouds shed, interact with the surrounding flow, and trigger the formation of a cascade of smaller, three-dimensional structures. The result is a highly dynamic process that showcases the complexity and richness of cavitating flows.

 

Conclusion

Veryst captured the complex evolution of cavitating wedge flows using high-fidelity computational fluid dynamics. Simulations like these provide valuable insights into unsteady multiphase flow behavior, helping engineers predict cavitation onset, assess structural risks, and guide the design of more efficient and reliable fluid systems.

T. Hu, H. Wang, and H. Gomez. “Direct van der Waals Simulation (DVS) of Phase-Transforming Fluids,” Science Advances, 9 (13): eadg3007, 2023