Technical Challenge
Capillary filling is increasingly utilized in microfluidic devices, where the autonomous movement of liquids driven by surface tension and wetting effects within hydrophilic microchannels enables both pump-free and precise fluid transport. These capabilities make capillary filling desirable for applications in MedTech, surface cleaning in semiconductor manufacturing, and reaction control in chemical production.
However, achieving robust, repeatable, and controllable capillary filling performance poses significant technical challenges. The dynamics of capillary filling are highly sensitive to factors such as surface wettability, channel architecture, and fluid properties; even minor variations can lead to substantial changes in flow rate, reproducibility, and meniscus stability. Understanding these filling dynamics plays a crucial role in the design and optimization of microfluidic devices.
Veryst Solution
The computational fluid dynamics (CFD) and multiphase flow experts at Veryst developed multiphysics simulations to predict the dynamic capillary filling of an L-shaped microchannel with water. The microchannel is initially filled with air. We used a multiphase flow formulation coupled with dynamic wetting theory to capture the complex interfacial dynamics between air and water, as well as the temporal evolution of the three-phase contact line. By varying the contact angle, we quantified how surface wettability influences the capillary filling process.
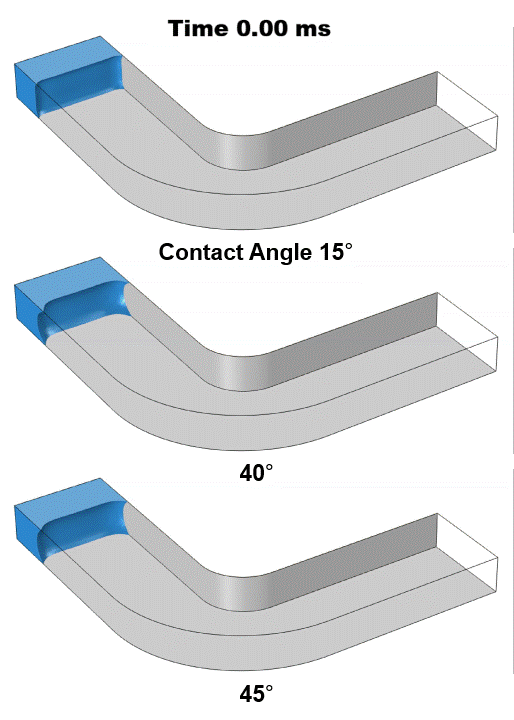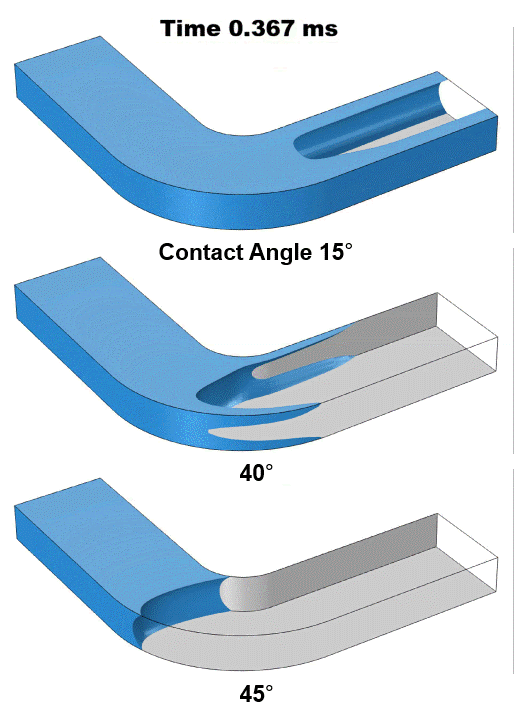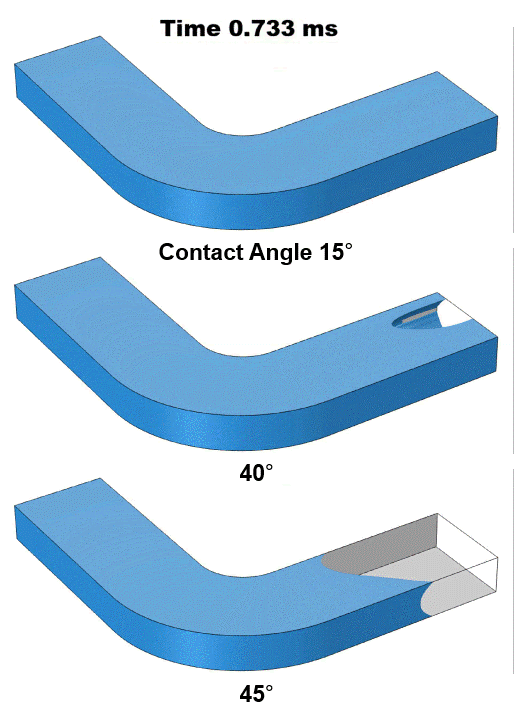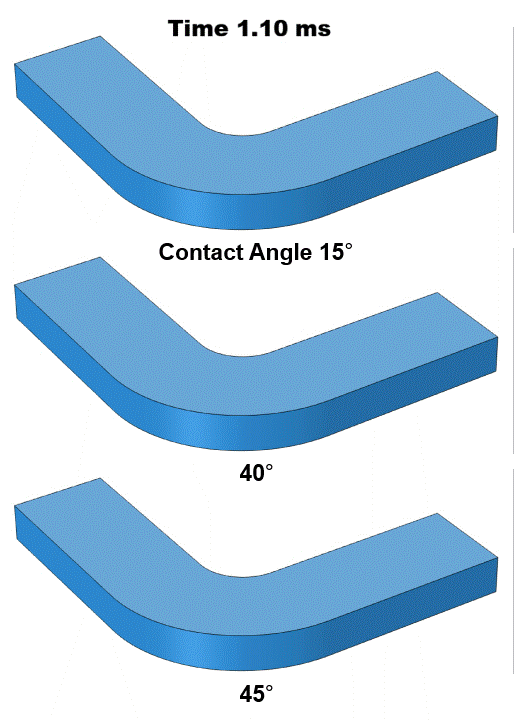
We first analyzed an ultra-hydrophilic surface with a contact angle of 15° (Figure 1 top row). Because the channel walls have a strong affinity for water, water quickly advances along the walls, forming a U-shaped liquid–air interface that rapidly pulls water into the channel. Increasing the contact angle to 40° (Figure 1 mid row) produces a noticeably slower filling process. Although the three-phase contact line still advances faster than the bulk liquid–air interface, its overall speed is lower compared to the ultra-hydrophilic case, resulting in less interface curvature. When the contact angle is further increased to 45° (Figure 1 bottom row), the filling changes dramatically. In this case, the contact line and the liquid–air interface advance at comparable speeds, maintaining a stable capillary meniscus shape throughout filling.
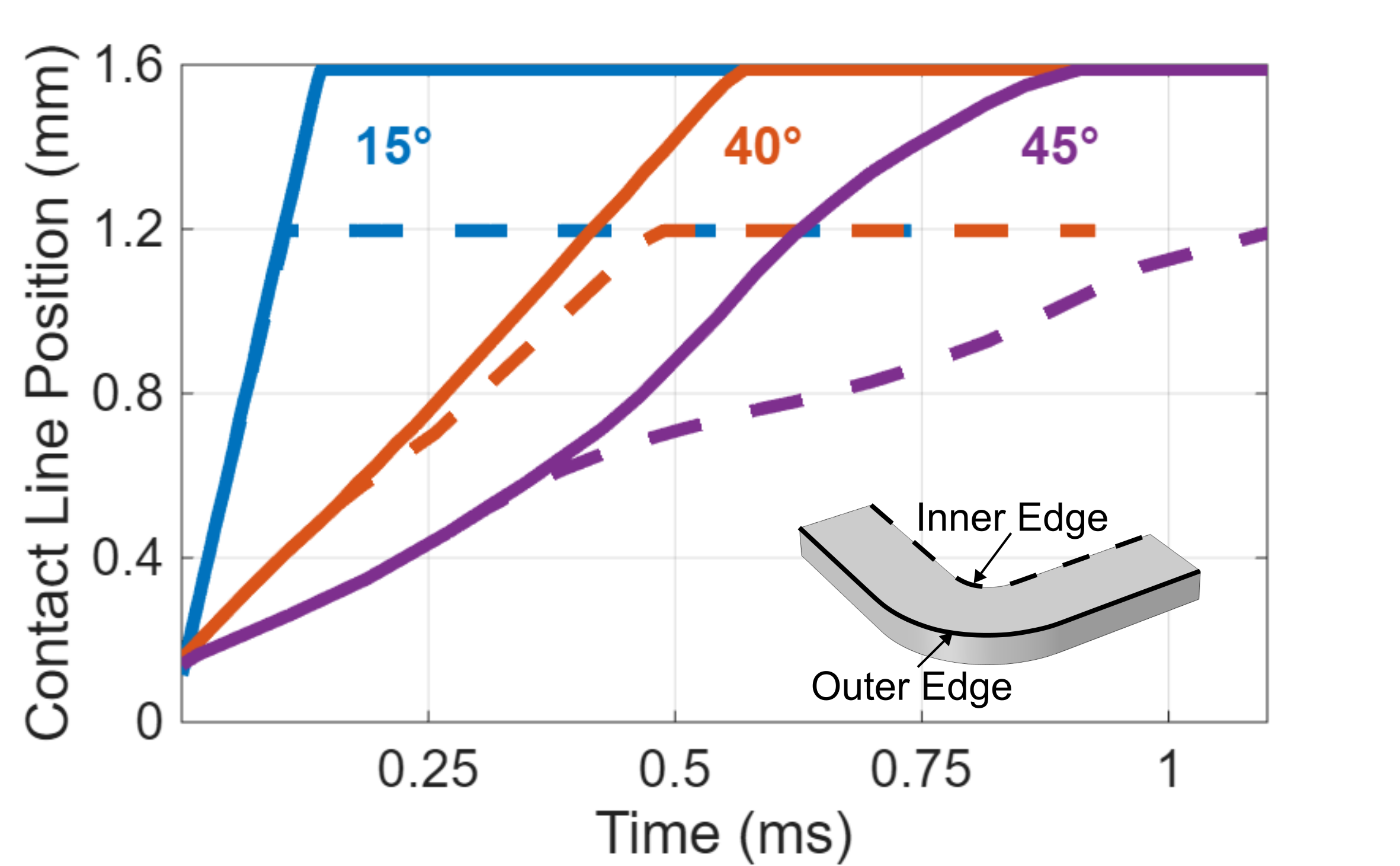
Figure 2 shows the contact line positions at the inner and outer channel walls as a function of time. For a contact angle of 15°, the contact line moves at nearly the same velocity along both walls until the channel is filled. As the contact angle increases to 40°, the contact line initially advances at similar rates along the inner and outer walls. However, as the fluid approaches the elbow region, motion along the inner wall slows slightly while that along the outer wall maintains its speed. If we further increase the contact angle to 45°, the liquid–air interfacial energy begins to dominate over solid–liquid adhesion. Upon entering the curved region, the motion of the contact line along the outer wall accelerates while that along the inner wall decelerates, resulting in the inner and outer contact line positions reaching the end of the channel at approximately the same time.
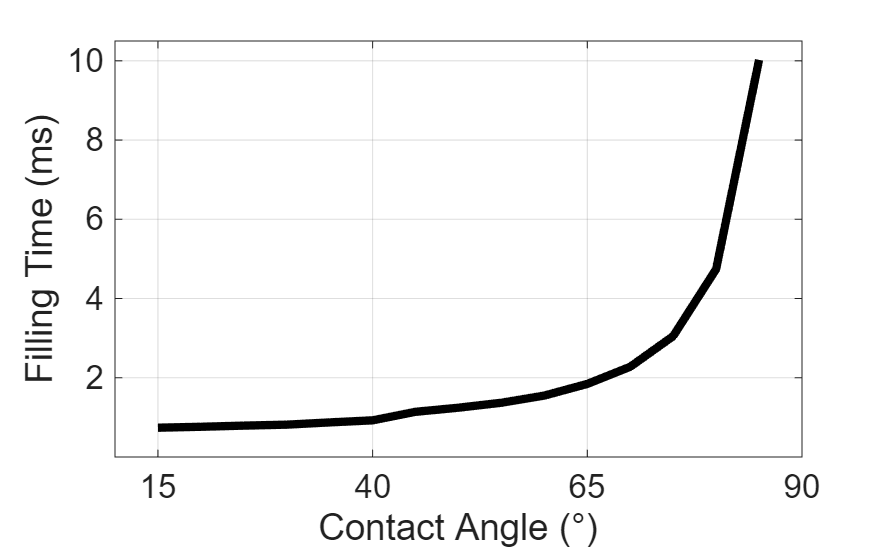
To further quantify this sensitivity, Figure 3 shows the filling time as a function of contact angle. The results reveal an exponential increase in filling time with contact angle. As the contact angle approaches 90°, the filling time tends toward infinity, consistent with the absence of capillary forces to drive the liquid–air interface.
Conclusion
Veryst successfully captured the sensitive and complex interfacial dynamics of capillary filling using high-fidelity multiphase computational fluid dynamics (CFD) simulations. Our results provide crucial guidance for the design and optimization of microfluidic devices that rely on precise capillary-driven fluid handling, enabling engineers to tailor channel geometry and surface properties for accurate, efficient, and reliable capillary filling.