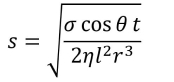Technical Challenge
Porous materials such as rock, soil, wood, and ceramics imbibe (absorb) fluid by capillary action. Capillary imbibition can be desirable in certain contexts, as in inkjet printing and water purification, and undesirable in others, such as moisture uptake in construction materials. Predicting and controlling fluid flow through a porous medium is of great practical importance.
One way to control the rate of imbibition is to tailor the geometry of confining, impermeable boundaries. This can be readily achieved, for instance, in paper-based micro- and milli-fluidic devices by designing channels of varying cross section. Prototyping and testing different channel geometries can be time- and cost-intensive, motivating the need for simulation-based guidance to accelerate and improve new experimental designs.
Veryst Solution
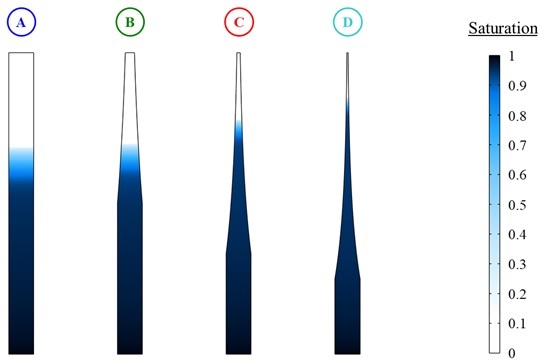
Veryst combined computational fluid dynamics (CFD) with a phase transport model to predict the rate of capillary imbibition (flow) in paper-based fluidic devices with complex channel geometries. This type of device is relevant to paper chromatography where it is desirable to separate the rate of imbibition between two compounds. We simulated four different devices with exponentially converging cross sections, and the degree of liquid saturation in each device was monitored as a function of time.
Figure 1 shows the simulation results after 40 seconds of fluid uptake in each device. Device A is a straight channel of length 60 mm, width 5 mm, and depth 1 mm. Devices B-D are designed with the same length and depth, but exponentially contract in width over successively shorter distances. As the rate of spatial contraction increases, fluid flows further into the porous medium in the same timeframe. This is indicated in Figure 1 by the extent of fluid ingress into each device along the flow direction.
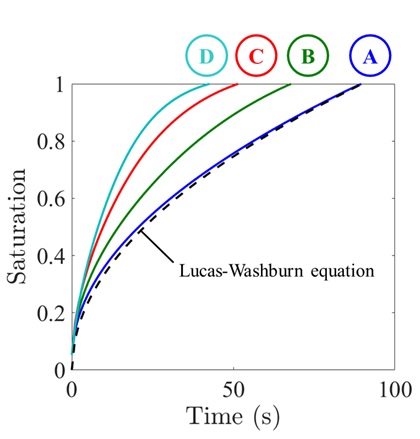
For a straight channel (device A in Figure 1), the Lucas-Washburn equation predicts that the liquid saturation in the porous material, s, varies with the square-root of time, t:
where σ is the surface tension, η is the dynamic viscosity, θ is the contact angle, r is the average pore radius, and l is the channel length. The Lucas-Washburn equation agrees well with simulations of liquid saturation as a function of time in a straight channel (Figure 2). Devices with more sharply converging channels imbibe fluid at a faster rate compared to the straight channel, implying that the rate of imbibition through a porous material can be controlled by tailoring the flow cross section. Converging channels are expected to accelerate fluid flow, whereas expanding channels decelerate the flow.
Conclusion
Veryst used computational fluid dynamics (CFD) to test the effect of channel geometry on the rate of capillary imbibition in four paper-based fluidic devices, which can be used for chromatographic separation of multicomponent mixtures. Simulations such as these can help predict fluid flow in porous media and suggest new avenues for flow control, which ultimately saves on time, cost, and materials in practical applications.