Technical Challenge
The pop and jump functionality of rubber jumpers relies on the sudden release of stored elastic strain energy, which is converted to kinetic energy and allows the toy to jump. However, the inversion and subsequent jump of the jumper is a highly nonlinear problem involving finite elastic deformations, metastability, contact, and transient dynamics. To assess the mechanics of the toy and the jumping, it is essential to capture all nonlinear phenomena present in the system, which is only possible through accurate modeling of the rubber material.
Veryst Solution
Veryst developed a nonlinear finite element solution that uses nonlinear material modeling for modeling the inversion and jump of a rubber jumper. The simulation accurately models the bistable (or multistable) deformation and replicates the jump when released from the inverted state. Bistable geometries are used in manufacturing, haptics, and consumer products to release energy or change the state of the system quickly, with little user input.
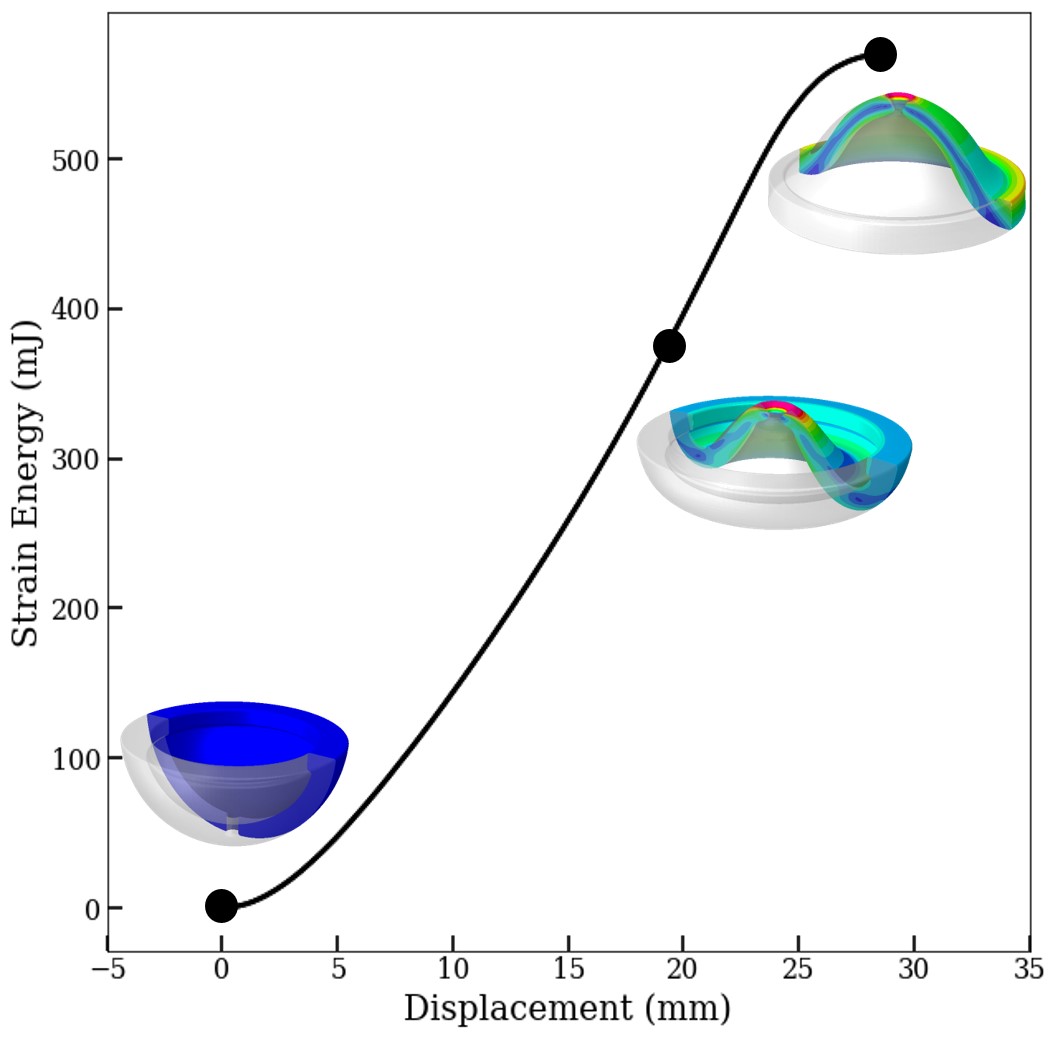
The inversion of the rubber jumper, which ultimately flips the curvature of the original geometry, stores strain energy in the popper material in the form of elastic deformation. During the inversion of the jumper, which we explicitly model in our finite element model (see Figure 2), the strain energy gradually increases as strains and stresses continuously rise within the material. However, the strain energy reaches a local maximum point where the strain energy gradient is zero, as shown at 30 mm of displacement in Figure 2. This behavior, as predicted by our numerical simulation, provides a metastable state for the popper, allowing it to maintain the inverted position for a short period of time before vigorously snapping back to its original undeformed state, resulting in a sudden popping sound and jump.
In our simulation, we apply a small perturbation load immediately after the jumper’s inversion to induce the popper to revert to its original state. In the real world, geometric imperfections or slight non-symmetries in the way the actuator inverts are sufficient triggers for the popper to snap-back and jump.
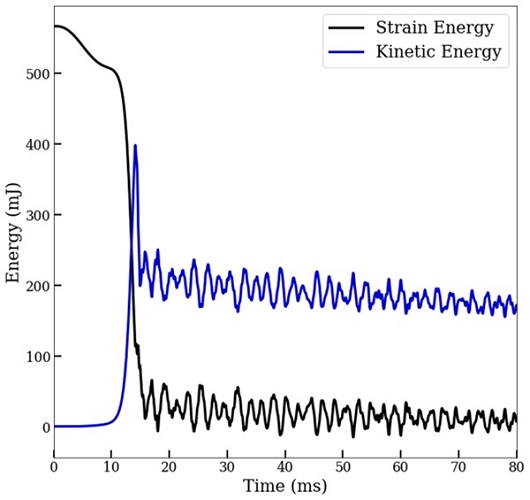
Figure 3 depicts the temporal evolution of the strain and kinetic energy for the entire jumper geometry during the jump-back to its original state, as predicted by our finite element model. At t=0 s, all energy is stored as strain energy and the kinetic energy is equal to zero. However, within 5 ms, strain energy rapidly decreases as it is converted to kinetic energy. Ultimately, after the snap-back of the jumper and the impact with the ground, strain energy oscillates around the 0 strain energy state and the popper continues to travel upwards with a decreasing velocity due to the influence of gravity. Some of the energy in the jumper is dissipated through material effects, as well as due to contact with the ground.
In Figure 4 and the video in Figure 5, we compare the predictions from our FEA model to our experimental observations while recording a slow-motion, high-speed video of the “jump” of the toy. Despite the geometric imperfections that are present in the real jumper, the FEA predictions are very similar to the experiments, particularly in the timing of inversion and the duration of the jump. The timing inversion and the duration of the jump are primarily driven by the behavior and stiffness of the jumper material, indicating that our model of the material’s behavior in our simulation captures the important effects for this problem.