Technical Challenge
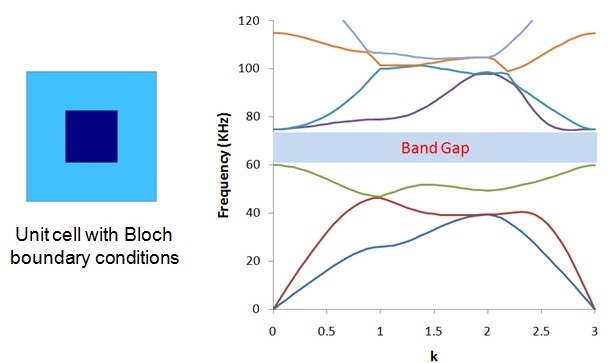
There is a growing demand for applications utilizing periodic band gap structures. Optimizing the location and width of the band gap is most efficiently performed using an eigenfrequency analysis of the unit periodic cell with Floquet (or Bloch) boundary conditions.
This analysis requires a complex solver due to the nature of the Floquet boundary conditions (not due to damping). This capability was not readily available in commercial finite element analysis software.
Veryst Solution
Veryst developed a unit cell model of the two materials making up the phononic structure in COMSOL Multiphysics. We implemented the Floquet boundary conditions in equation form and performed a complex eigenfrequency analysis spanning all wave numbers covering the irreducible Brillouin zone.
We used the finite element model to optimize the width and location of the band gap. The plot of the natural frequencies, in Figure 1, shows the location of the band gap for a specific cell configuration.
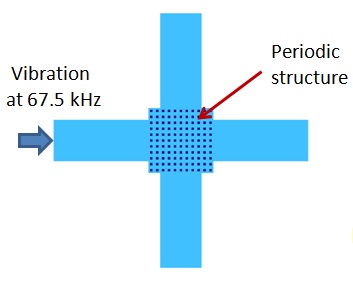
Figure 2 is an example that illustrates the effectiveness of the phononic band gap structure in isolating vibrations in its band gap frequency range.
The animation in Figure 3 shows the harmonic response of the structure when excited at the left end at 67.5 kHz. The vibration of the left end is effectively isolated from the rest of the structure.