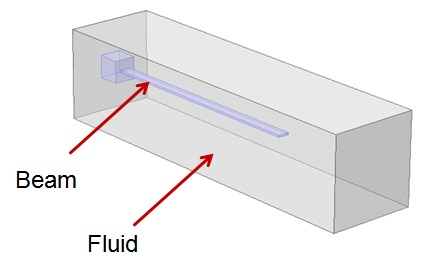
Technical Challenge
The natural frequencies of thin structures such as beams, plates, or shells change when immersed in a fluid. The fluid also affects mode shapes and provides additional damping.
This phenomenon affects structures across a wide range of industries and sizes, from micro-scale structures such as MEMS actuators to larger structures such as ships.
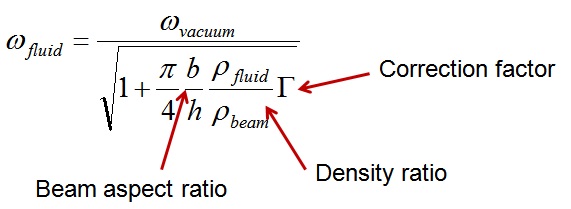
In the case of immersed beams, an approximate analytical solution of the form shown in Figure 2 is frequently used to estimate the immersed natural frequencies based on the fluid properties, beam geometry, and the structure-only natural frequencies.
The analytical expression accounts for the “added mass” of the fluid that is displaced by the beam as it vibrates. However, this approach is approximate and the correction factors provided are specific to cantilever beams.
Veryst Solution
Veryst uses COMSOL Multiphysics to determine the natural frequencies and mode shapes of an immersed cantilever beam and compare the results with the “added mass” approximation. We set up this problem as a coupled acoustic-structure eigenvalue analysis. We used a pressure acoustics formulation, since thermal and viscous losses are negligible for this beam size. For smaller beams where this assumption is not valid we would use a different formulation that accounts for these effects, such as the thermoviscous acoustics formulation in COMSOL Multiphysics.
The first and fourth natural frequencies (in Hz) of beams in vacuum, air, and water are shown in Table 1. The results show, as expected, that air has a minor effect on the beam and water reduces the lowest natural frequencies of the beam by about 20%.
The analytical estimate for a beam immersed in water is also shown in the table and is close to the COMSOL prediction for this relatively standard beam configuration.
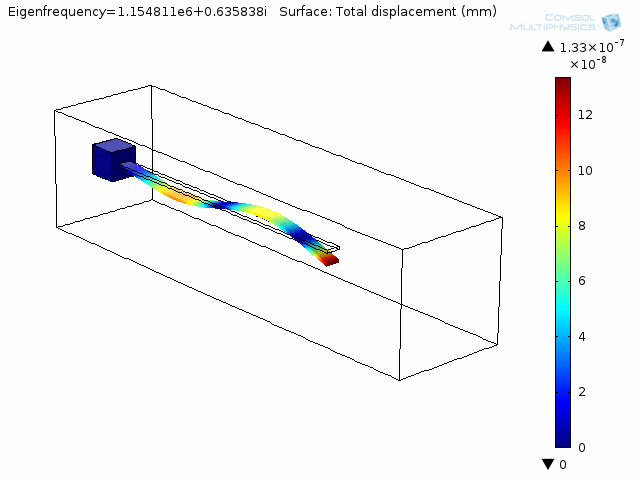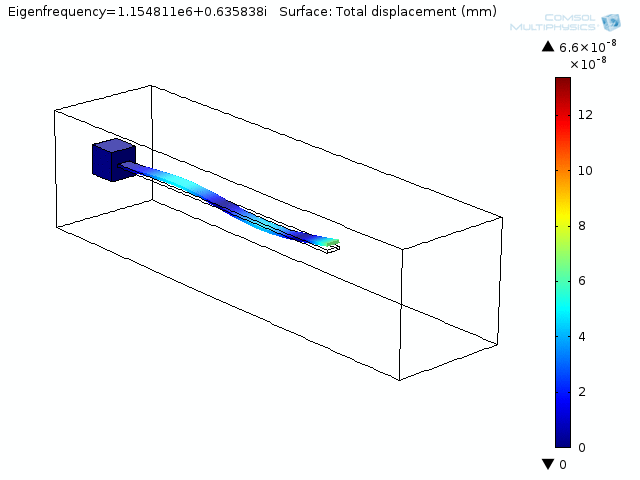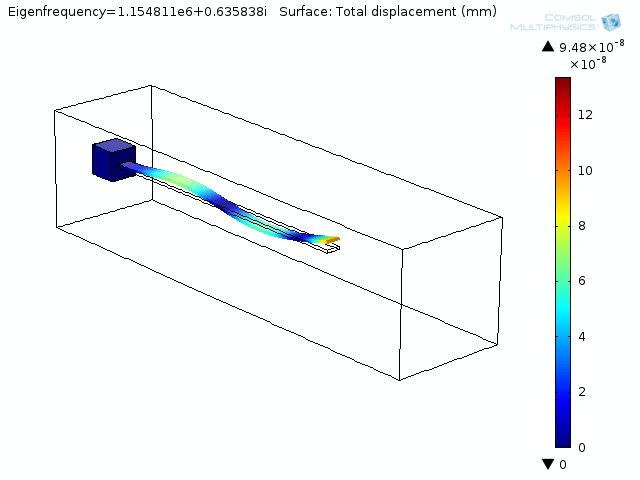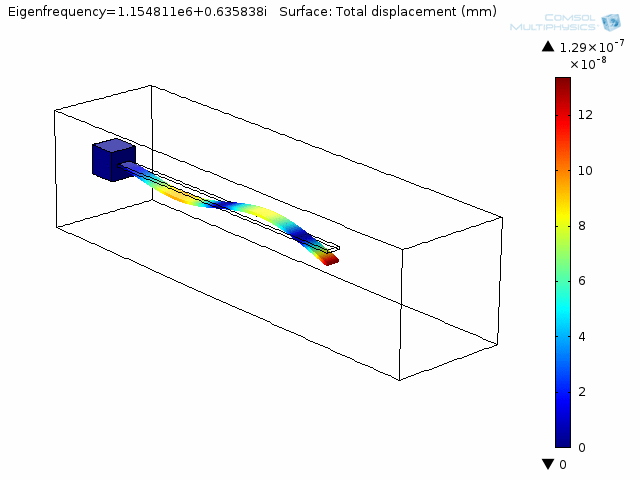
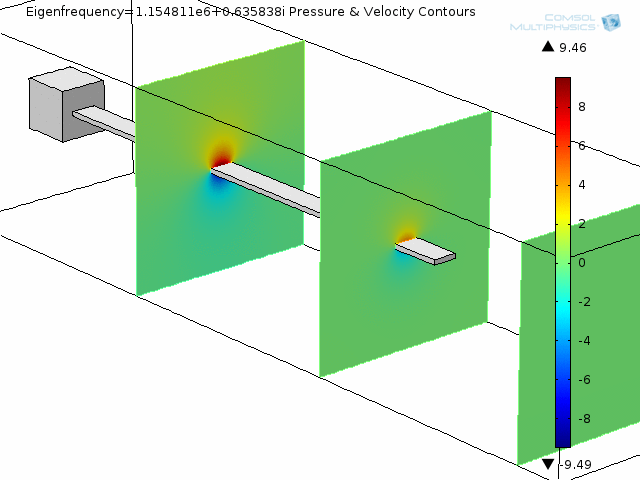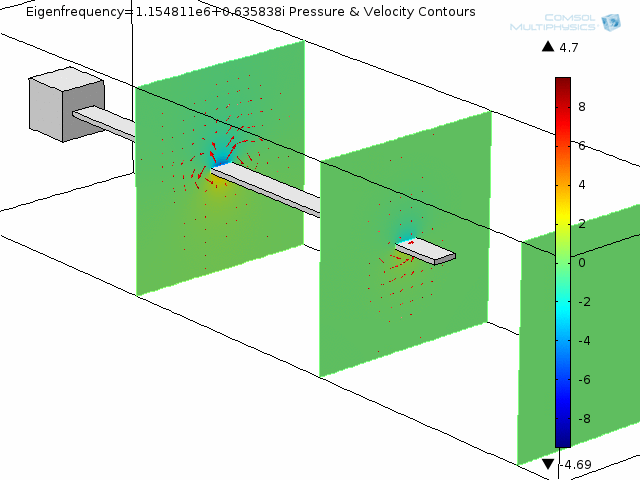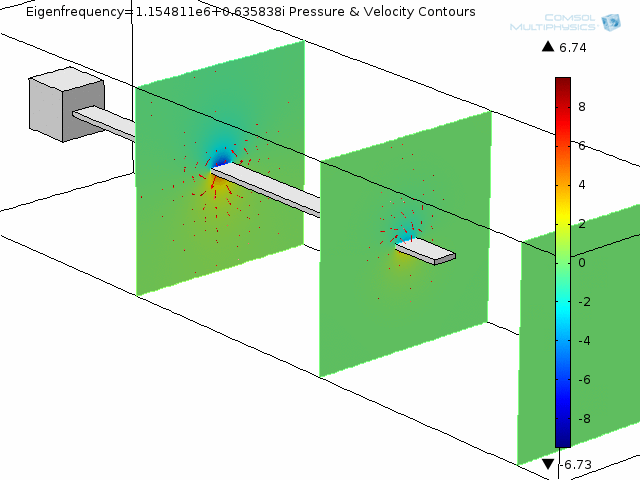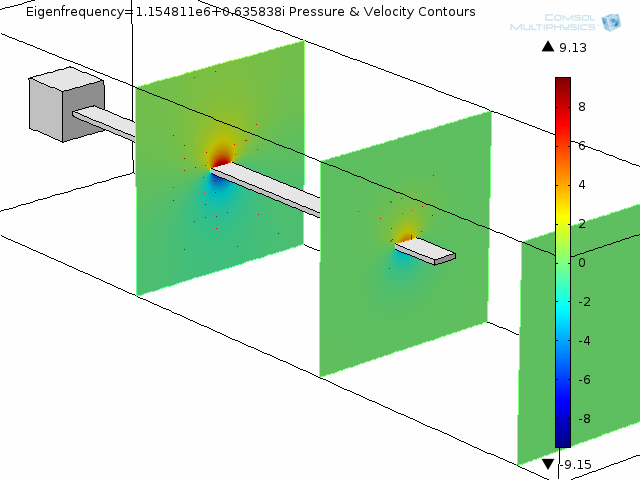
The animation below shows the fourth mode of deformation for a beam immersed in water.
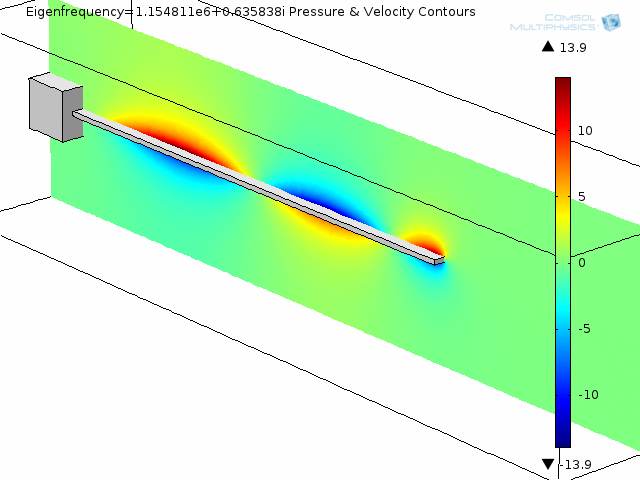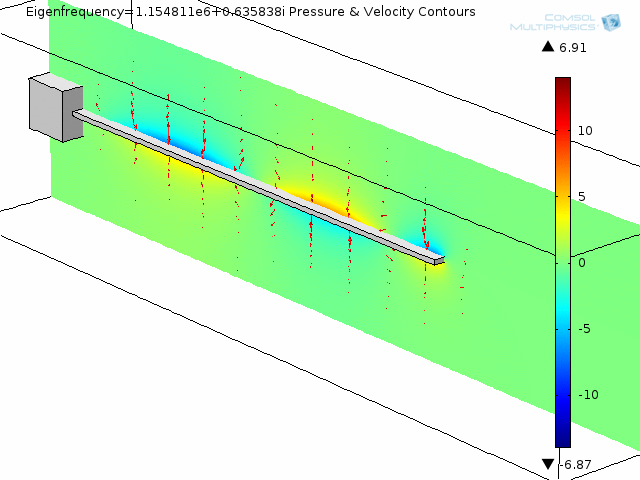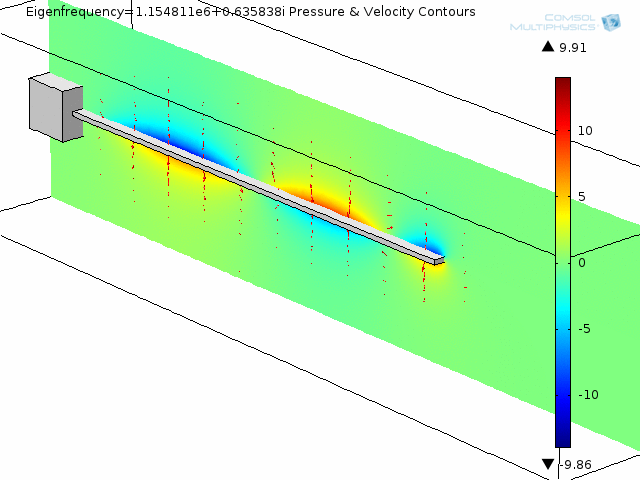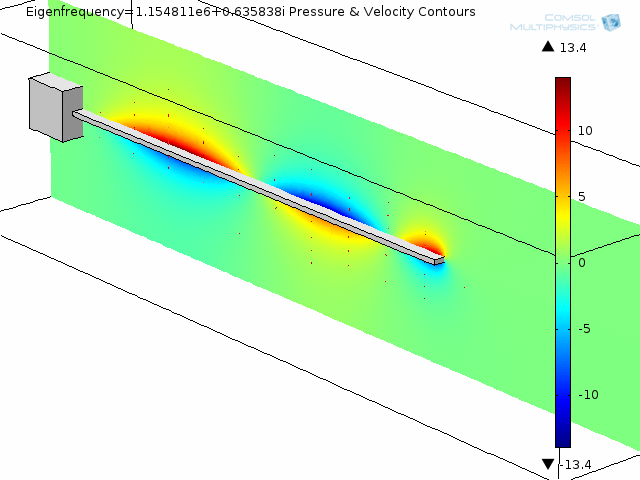
The next two animations show fluid pressure contours and fluid velocity arrow plots at two slices along the beam, also for the fourth mode shape.
This example involved a simple cantilever immersed in fluid to illustrate the concept of immersed beam vibration. However, the same coupled structural-acoustic modeling approach is applicable to more complex geometries, such as ship hull vibrations.
With minor modifications, this approach can also be applied to cases where the fluid is not stationary, such as flow in flexible pipes.