Micromixing in a Multi-Inlet Vortex Mixer

Flash nanoprecipitation is an efficient approach for high volume manufacturing of nanoparticles, such as the lipid nanoparticles found in mRNA vaccines, that relies on continuous turbulent mixing.  Various mixer technologies have been designed to introduce inlet streams containing the nanoparticle components such that they meet and rapidly mix.  Under the right mixing conditions, the solution carrying the lipid particles becomes supersaturated, causing the lipids to precipitate and encapsulate the active organic molecule.

The formation of lipid nanoparticles (LNP) is sensitive to the mixing rate, as the assembly process is a competition between aggregation, which dominates at slow mixing rates (>100 ms), and nucleation/growth, which dominates for fast mixing.

We simulate such a mixing process in a multi-inlet vortex mixer to determine the sensitivity of the mixing rate to the inlet flow rates.

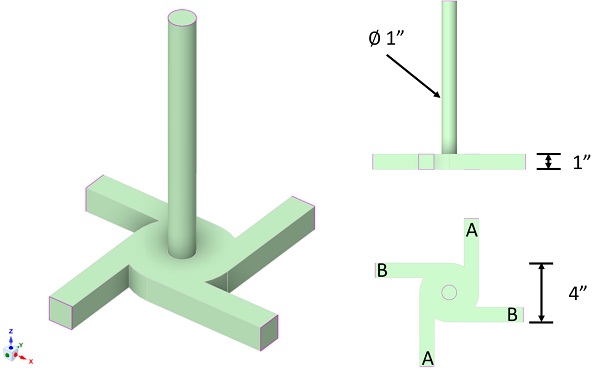
The multi-inlet vortex mixer (MIVM), shown in Figure 1, permits the independent variation of inlet streams to control micromixing and supersaturation.  In this study, we fix the ratio of the volumetric flow rate between the aqueous (A) and organic (B) streams to a value of 4:1.  The aqueous inlet stream is pure water and the organic inlet stream is pure ethanol.  We define a Reynolds number to characterize the flow inside of the mixer as an average of the inlet stream Reynolds numbers

where n is the number of inlets to the mixer, ρ_i is the density, u_i is the velocity, D is the chamber diameter, and μ_i is the viscosity of the i^th inlet stream.

While the design of the MIVM is simple, the fluid mechanics of the mixing are difficult to predict analytically.  Challenges include the complex material properties of water-ethanol mixtures, which exhibit unique behavior as they are mixed.  The viscosity of these mixtures varies such that the mixture viscosity at intermediate compositions is larger than either of the pure component viscosities.  We use a model that Veryst developed to capture accurately the mixture viscosity as a function of mixture composition.¹

The design of the MIVM also promotes anisotropic turbulent structures to form as the streams meet inside the mixing chamber.  We utilize Large Eddy Simulation (LES) to capture accurately these structures and predict the rate of mixing. 

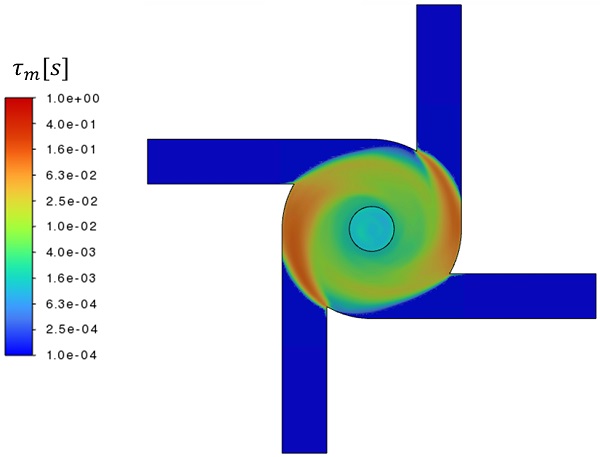
The animation in Figure 2 shows the mass fraction of ethanol plotted on two planes for Re = 7,500.  Large scale eddies form as the inlet streams meet in the mixing chamber.  The Schmidt number, which is the ratio of momentum diffusion to mass diffusion, is on the order of 1,000 for water-ethanol mixtures.  This indicates that the mixing will initially occur in thin layers, which can be seen in the large eddies that form as the streams enter the mixing chamber.  The large eddies break down into smaller eddies, where dissipative mixing, called micromixing, dominates.  It is at these small scales that the rate of mixing competes with the aggregation and nucleation/growth processes.

We define the micromixing timescale as the ratio of the ethanol mass fraction variance to the ethanol mass fraction dissipation rate.  We extract the variance directly from the transient simulation, while the dissipation rate is computed based on the eddy diffusivity and gradients of the filtered mass fraction field.  Figure 3 shows the time-averaged micromixing timescale for the baseline case plotted on the horizontal midplane of the mixing chamber.  The volume-averaged micromixing rate in the chamber is approximately 20 ms, which is typically sufficiently fast to generate uniform particle distributions.

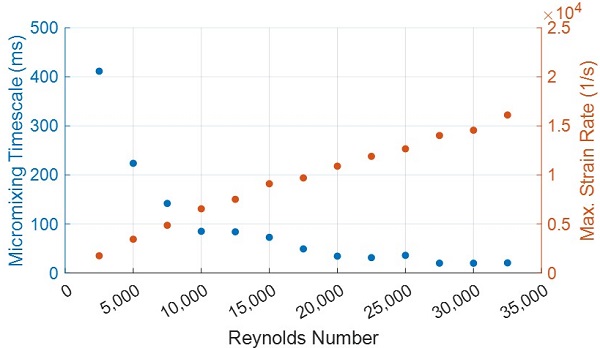
Finally, we run a parametric sweep over the Reynolds number to assess the minimum flow conditions required to produce a sufficiently fast micromixing rate.  As shown in Figure 4, the average mixing rate is below 100 ms for Reynolds numbers greater than 10,000 and decreases slowly for Reynolds numbers greater than 20,000.  Conversely, the maximum fluid strain rate in the chamber increases roughly linearly with the Reynolds number and may adversely affect the nanoparticles if they are shear sensitive.

Conclusion

Veryst was able to predict micromixing rates in a multi-inlet vortex mixer for lipid nanoparticle production using high-fidelity computational fluid dynamics (CFD). Simulations such as these can help predict minimum flow rates required to produce desired nanoparticle size distributions while avoiding potentially damaging flow shear stresses.