Safe Distance? A Simulation of the Trajectory of Exhaled Droplets

Social distancing—keeping a distance of at least 2 meters (approximately six feet) between individuals from separate households—is recommended as one of the most important ways to help reduce the spread of COVID-19¹.  This distance comes from an understanding of the behavior of droplets emitted by coughing, sneezing, and even talking.  Understanding how far and how fast droplets disperse into the surrounding air is a complex challenge which has been investigated thoroughly by public health experts to enact policies that can help curb the spread of disease.
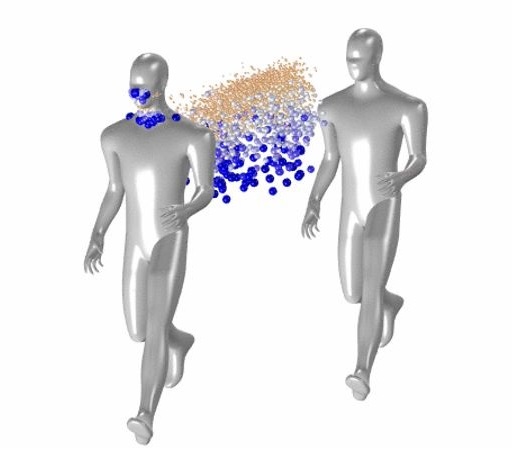
In this problem, we investigated the trajectory of droplets from two runners in tandem, running at a moderate pace 2 meters apart.  We considered how droplets emitted from the mouth travel from individuals breathing at a normal rate and without a mask.  Note that we did not investigate the transmission of potentially disease-carrying droplets within the respiratory tract, and instead defer to the experts at the Center for Disease Control and the World Health Organization.
 

Veryst used CFD (computational fluid dynamics) to simulate the trajectory of emitted droplets, including the multiphysics effects of droplet evaporation and drag forces, as a function of droplet size and velocity. 

We assumed that the rate of droplet evaporation is a function of relative humidity (RH), the velocity of the droplet relative to air, and particle diameter.  This leads to a reduction in droplet mass which affects the drag and gravitational forces.  For numerical expedience, we assumed that droplets do not shrink beyond 20 µm.  (When droplets are smaller than this, they are typically considered aerosol particles and we treat them as mass-less particles².  Particles larger than 20 µm are considered droplets and we account for their mass as well as the drag forces acting on them.)

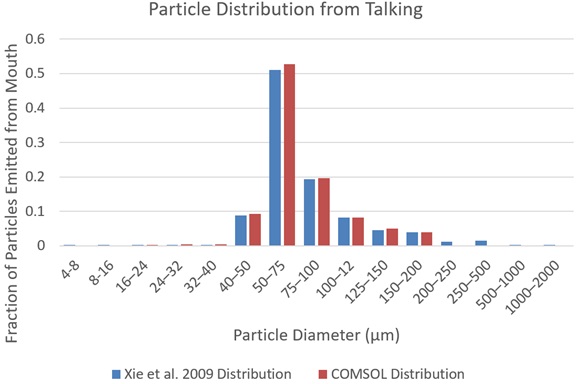
The initial distribution of the size of droplets from exhaling is shown in Figure 1, and is based on experimental results from the literature, where droplets were collected from individuals talking in a controlled environment³.

We did not model the effect of wind on droplet trajectory.  We only considered the flow of emitted droplets through moving air caused by running. 

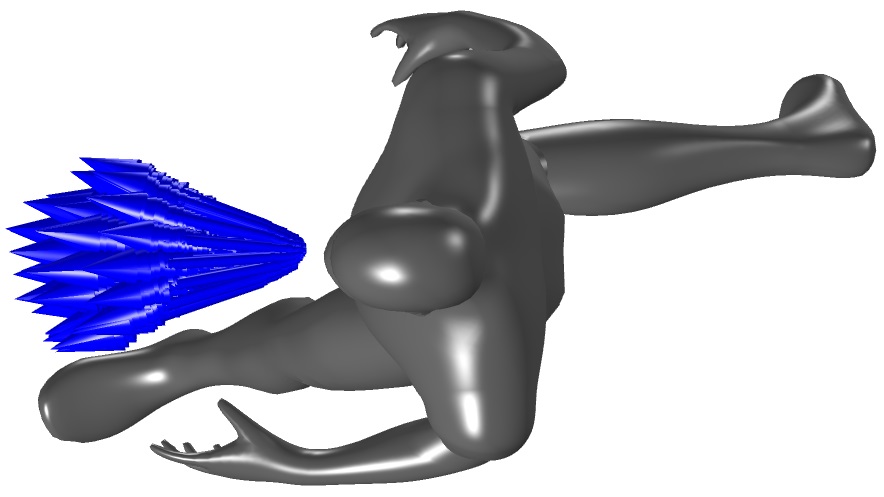
The exhaling stream of droplets was represented by a conical distribution of droplets with a cone angle of 30° (as shown in Figure 2) at a constant speed of 2.5 m/s (Re= 3.3×10³) relative to the movement of the individual, representing moderately deep breathing (as opposed to coughing or sneezing, which correspond to higher velocity exhalations)⁴.

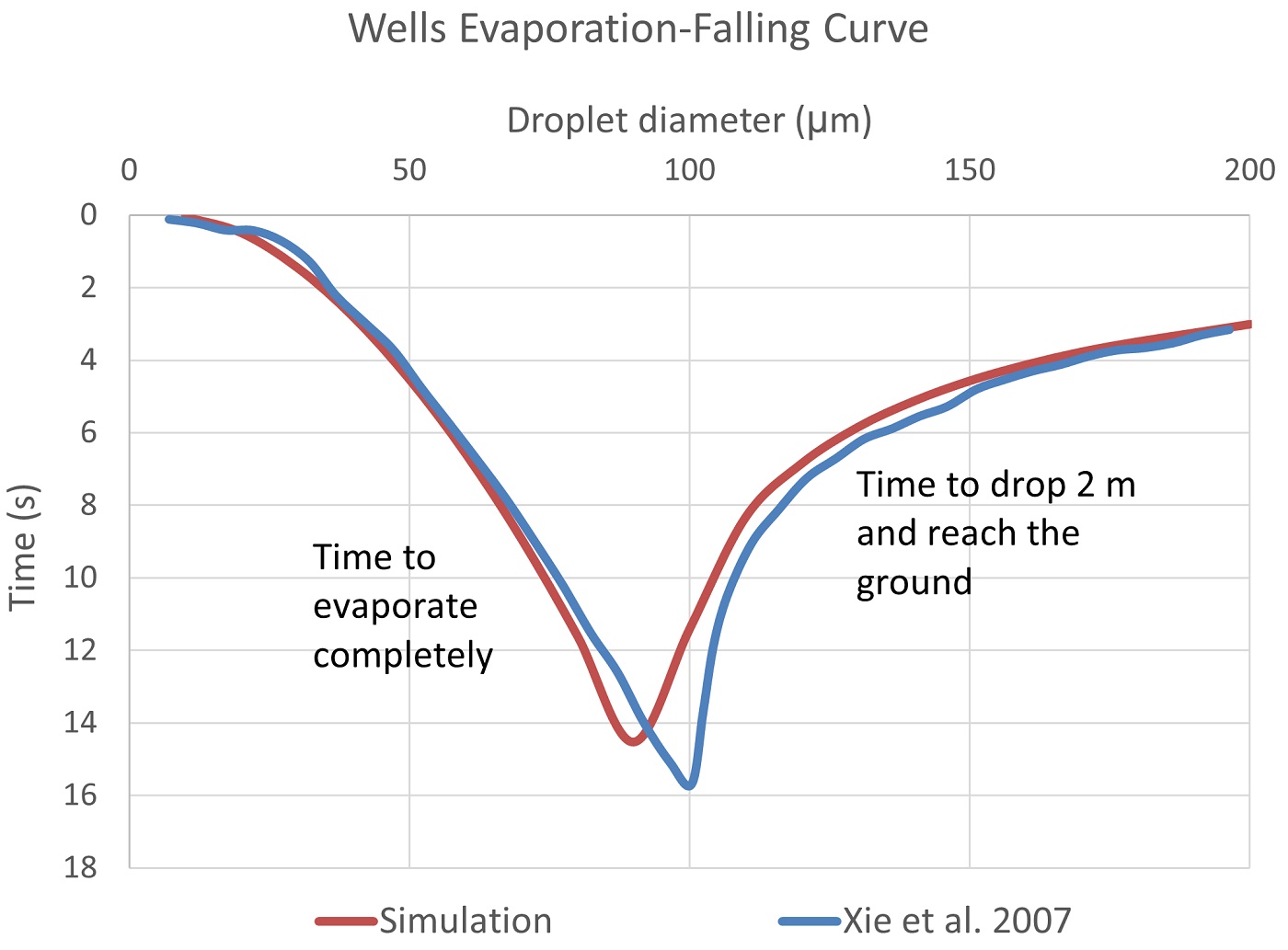
The challenge of modelling a non-isothermal jet of exhaled droplets has been studied extensively. We therefore calibrated our physical model of droplets to those analytical expressions for droplet behavior that have been validated experimentally. In experiments, particles are released from a height of 2 meters into stagnant air and end up either evaporating completely or reaching the ground, depending on the balance between gravity and evaporation.

Figure 3 shows the time it takes for free-falling particles of different diameters to evaporate completely or reach the ground before evaporation. This is known as the Wells evaporation-falling curve and is shown at 50% RH and an initial particle height of 2 meters⁵. As seen in the curve, larger droplets take less time to reach the ground, droplets around 100 µm evaporate right after reaching the ground, and smaller droplets evaporate completely before falling 2 meters to reach the ground. We used this relationship to calibrate the evaporation rate of particles exhaled in our models.

For the simulation of droplet trajectories surrounding two running individuals, we placed two people in tandem and 2 meters apart, facing and traveling in the same direction.  We assumed an oncoming air velocity between a fast walk (~ 2.5 mph) and a fast run (~ 9 mph).

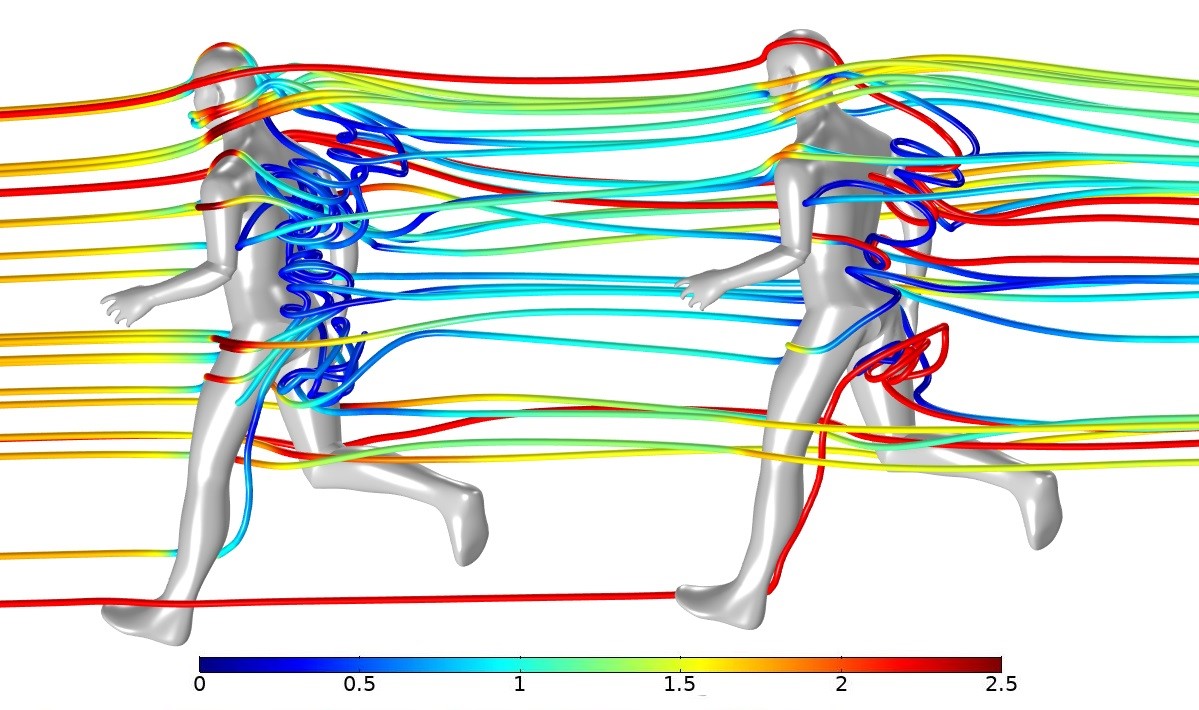
The air movement relative to the runners was modeled at 1.8 m/s (approximately 4 mph), as shown in Figure 4.  Our simulation predicts significant recirculation behind the runners.

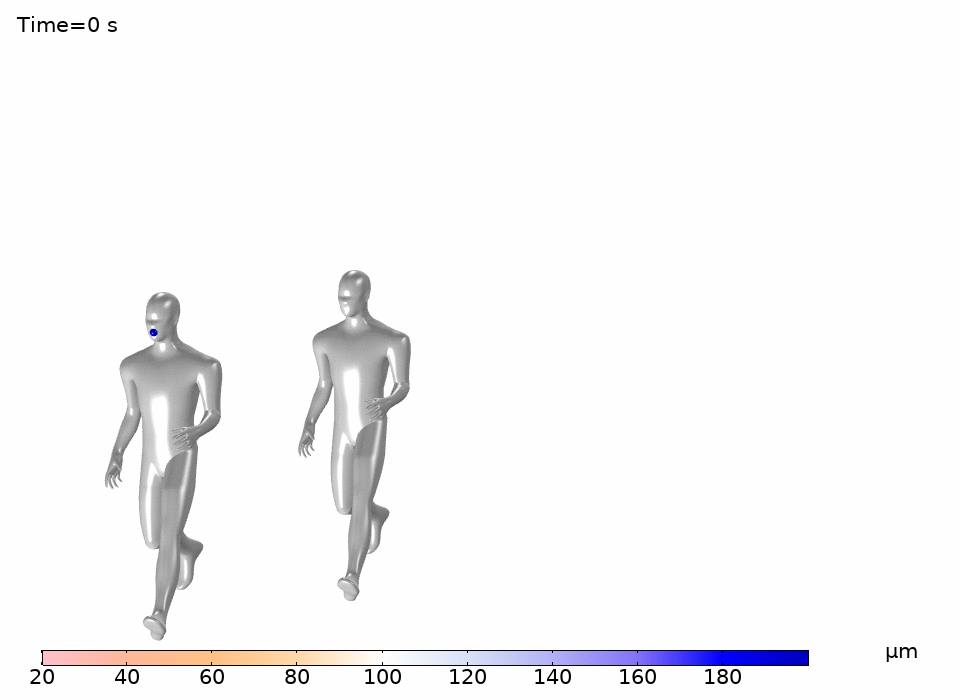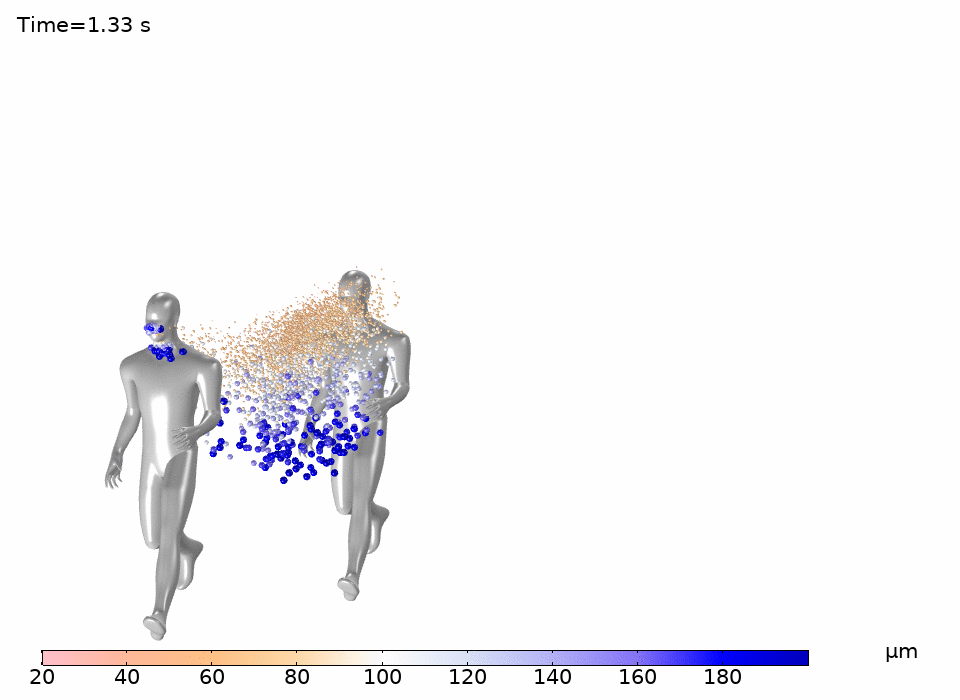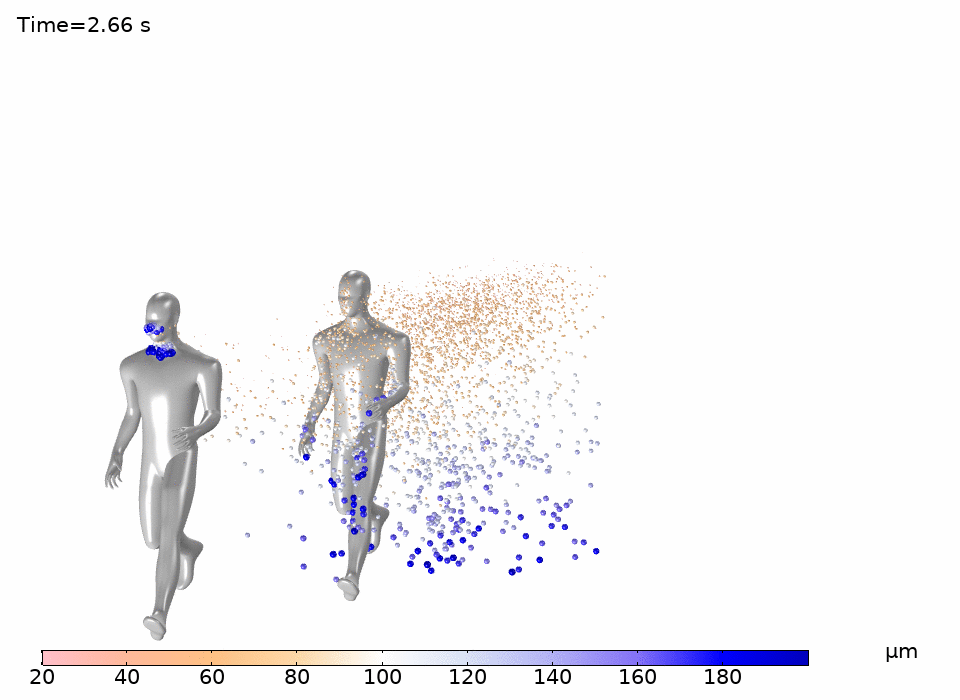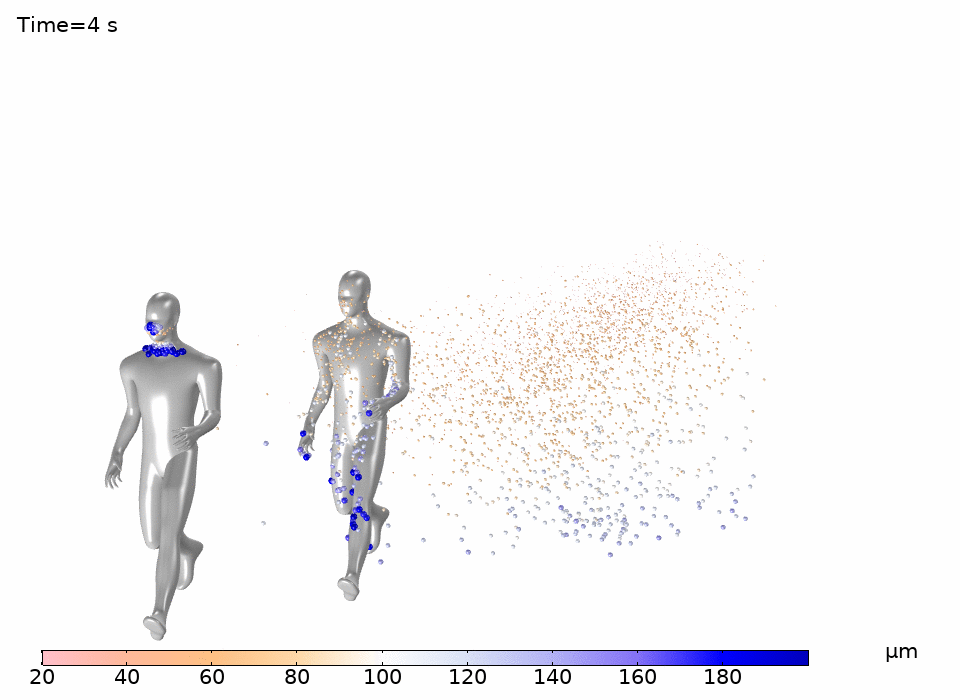
Figure 5 shows the trajectory of droplets from the first runner exhaling at 2.5 m/s relative to the movement of air.  In this model larger droplets quickly fall to the ground, while smaller droplets travel further. As seen in Figure 5, larger particles drop close to the rear runners’ legs while smaller particles are predicted to land on the rear runners’ face and torso.
 

Conclusion

Veryst simulated the droplet behavior from exhaling  for two runners travelling in the same direction while 2 meters apart.  This type of simulation provides a tool for evaluating droplet trajectories in other configurations of potential indirect disease transmission and developing guidelines that mitigate the spread of pathogens in airspaces. 

The model shown here demonstrates that larger droplets fall to the ground quickly while smaller droplets travel further.  Furthermore, small droplets can be easily carried by the surrounding air, and travel significantly farther than 2 meters.  These simulations illustrate the well-established fact that 2 meters is an unwise distance for running in tandem when the second runner is in the slipstream of the first.