Technical Challenge
It is frequently difficult to scale a chemical process from the laboratory to manufacturing. Scaling chemical reactors from the lab to pilot or production requires a detailed understanding of the physics within the reactor, which frequently involves fluid flow, mass transfer, reaction kinetics, and heat transfer. It is especially important to consider the type and degree of mixing when scaling reactors because these affect the local reaction rate and overall reactor yield.
This is particularly significant in reactors with additional relevant physics. For example, mixing affects cooling for strongly exothermic reactions and modifies the effective reaction area for multiphase and interfacial reactions. Transitioning from laminar flow to turbulent flow or increasing turbulent intensity in the flow increases the amount of mixing, even if the reactor geometry is qualitatively unchanged.
Veryst Solution
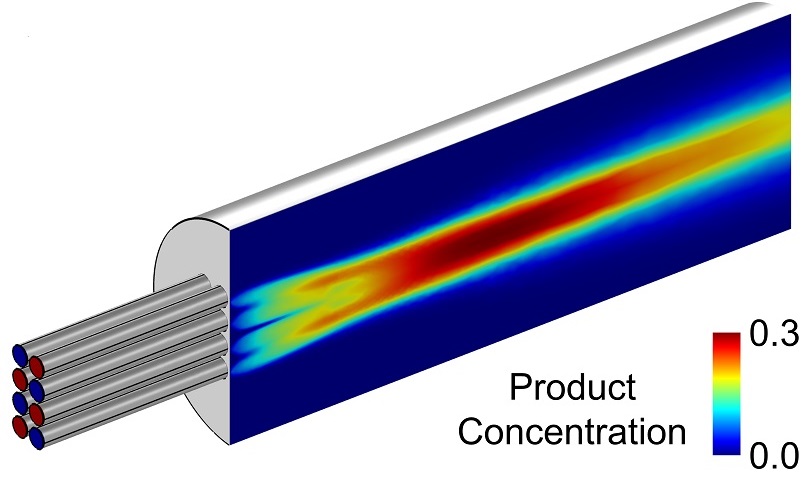
Veryst developed a multiphysics finite element model (in COMSOL Multiphysics) of a test reactor configuration to illustrate the effect of turbulent mixing on reactor size and yield (Figure 1). The model accounts for the transport of reactants and products due to molecular diffusion and flow (advection). We modulate the amount of laminar or turbulent mixing by changing the Reynolds number in the reactor. To simplify the analysis, we studied a simple diffusion-limited bimolecular reaction A+B→C. For certain laminar flows in this reactor design, we predicted poor mixing near the reactor inlet (Figure 1).
Laminar and Turbulent Flows
Mixing in a reactor is fundamentally different for turbulent and laminar flows. Whether a flow is laminar or turbulent is determined by the Reynolds number, which is the ratio of momentum transport by the flow (advection) to that by viscosity, Re = velocity × length scale / kinematic viscosity. The length scale is a characteristic length of the reactor geometry. Laminar flows are characterized by Re less than a few thousand, while turbulent flows are associated with higher Reynolds numbers. A laminar to turbulent transition region occurs between these limits and is dependent on reactor geometry, surface roughness, and the nature of the flow (oscillatory vs. steady).
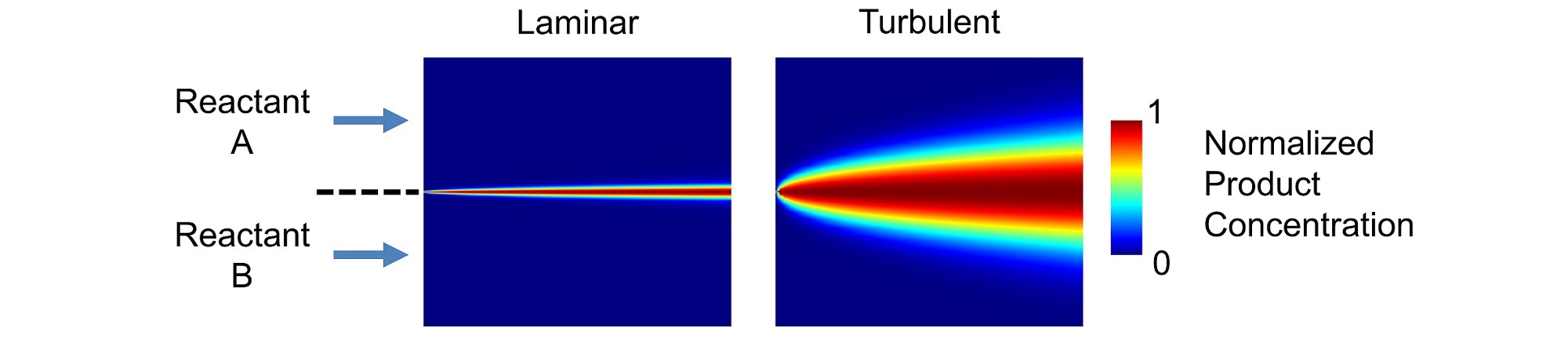
The turbulent intensity of a flow also depends on (and increases with) the Reynolds number. Turbulence dramatically increases mixing within a fluid, as shown in Figure 2 for the simple case of a biomolecular reaction in co-flowing streams. In the laminar case, the reaction occurs very close to the interface separating the reactants because mixing is dominated by molecular diffusion. Much more product is generated by the turbulent flow due to additional turbulent mixing.
Residence Time
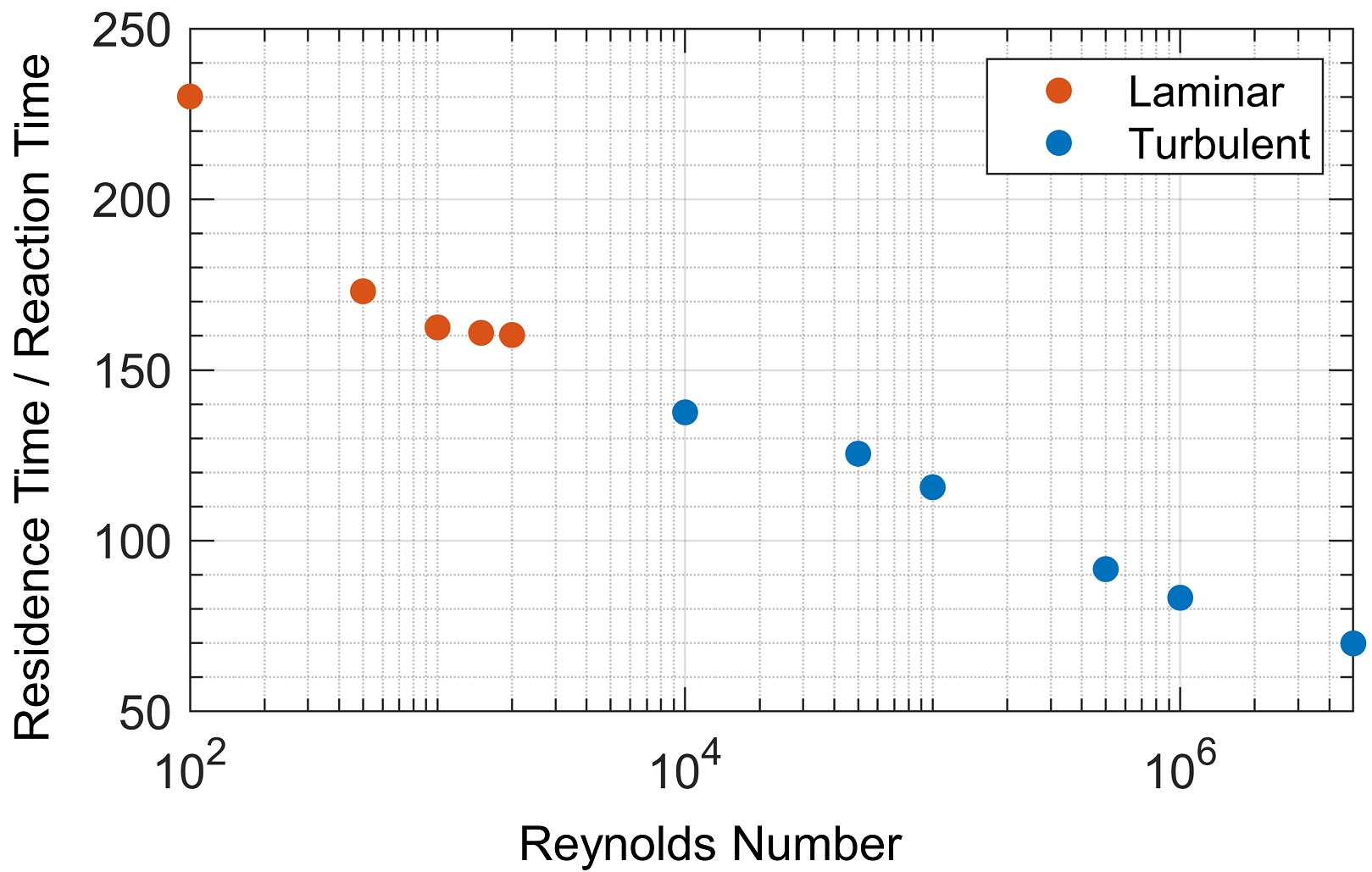
Estimates of scaled-up reactor sizes are often based on residence time. However, if mixing characteristics change with scale, reactors with equal residence times may produce different yields. Therefore, a detailed understanding of the transport processes in a reactor is required to size the reactor effectively. Figure 3 shows the residence time required to achieve 80% product yield for different Reynolds numbers. The required residence time decreases by a factor of four over the range of Reynolds numbers studied, indicating that increased turbulent mixing improves reactor efficiency.
Yield
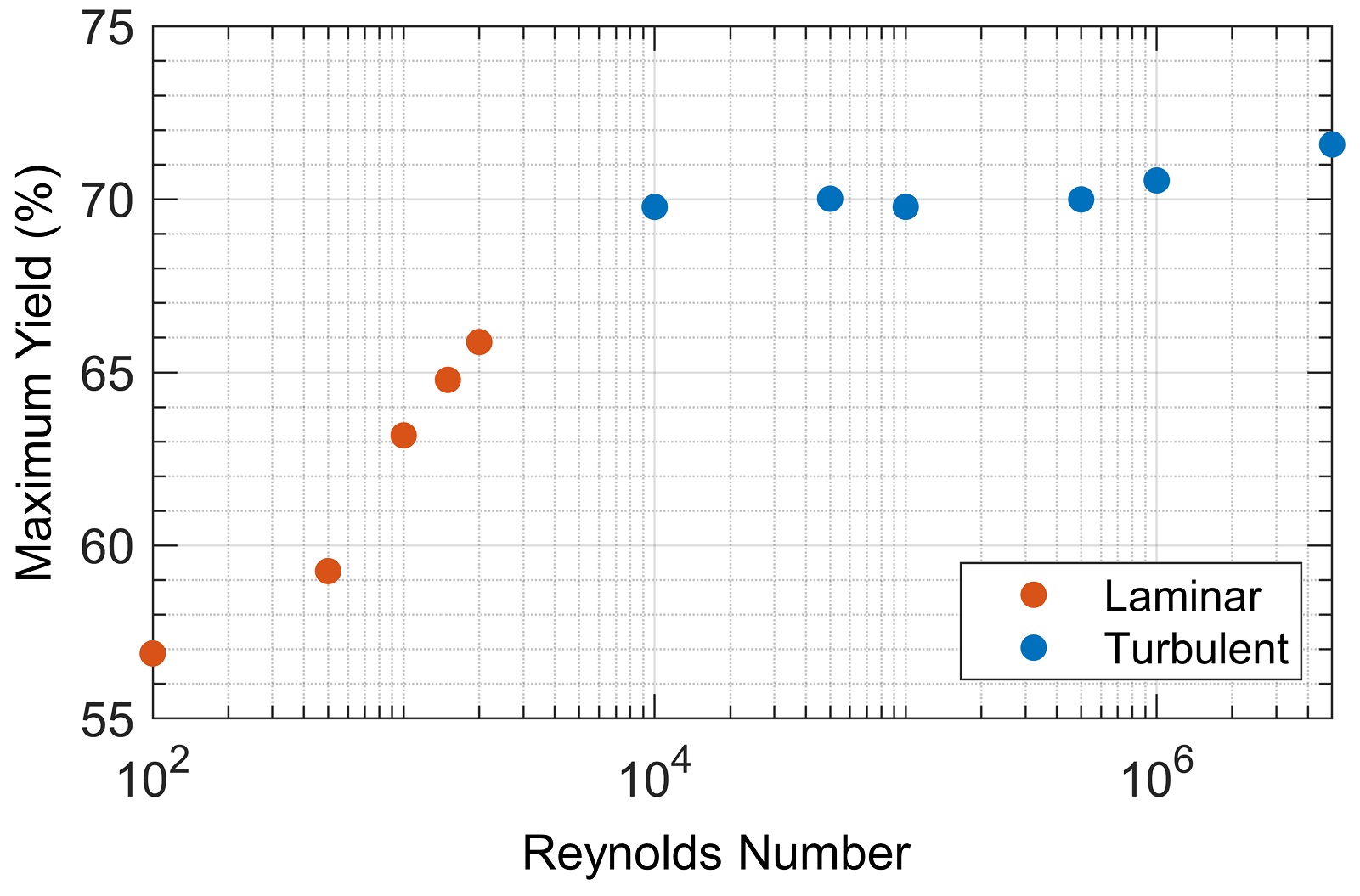
Mixing is especially important when designing reactors in which there are multiple reactions with different reaction orders. We considered the case where the product undergoes a decomposition reaction generating an undesired byproduct, C→D. In this case, the reactor size is limited by the decomposition reaction; if the reactor is too large then too much product will decompose. Therefore, the decomposition reaction sets a maximum possible yield (for an associated reactor size) that depends on mixing in the reactor and the rate of the decomposition reaction. In Figure 4, we show that the maximum yield increases with the Reynolds number until the transition to turbulence, after which the dependence is weak.
Conclusion
The size of a chemical reactor required to obtain a given yield depends strongly on mixing conditions within the reactor, which in turn depend on the reactor geometry and flow conditions. Mixing characteristics may change during reactor scale-up and dramatically affect reactor sizing estimates. This is especially important in reactors with additional relevant physics such as heating/cooling or multiphase mass transfer.
Modeling and simulation can provide deep insights into the transport processes in many types of reactors, informing design modifications for reactor scale up or optimization.