Technical Challenge
Microfluidic devices often contain solutions carrying multiple dissolved chemical species with varying concentrations. In many biochemical processes the challenge is to minimize the length of concentration gradients. In other cases, such as the synthesis of composite biomaterials or mimicking in vivo chemical gradients, the challenge is to produce long chemical gradients.
Controlling gradient length is often a critical device or process design feature and requires considering both fluid mechanics and mass transport.
Veryst Solution
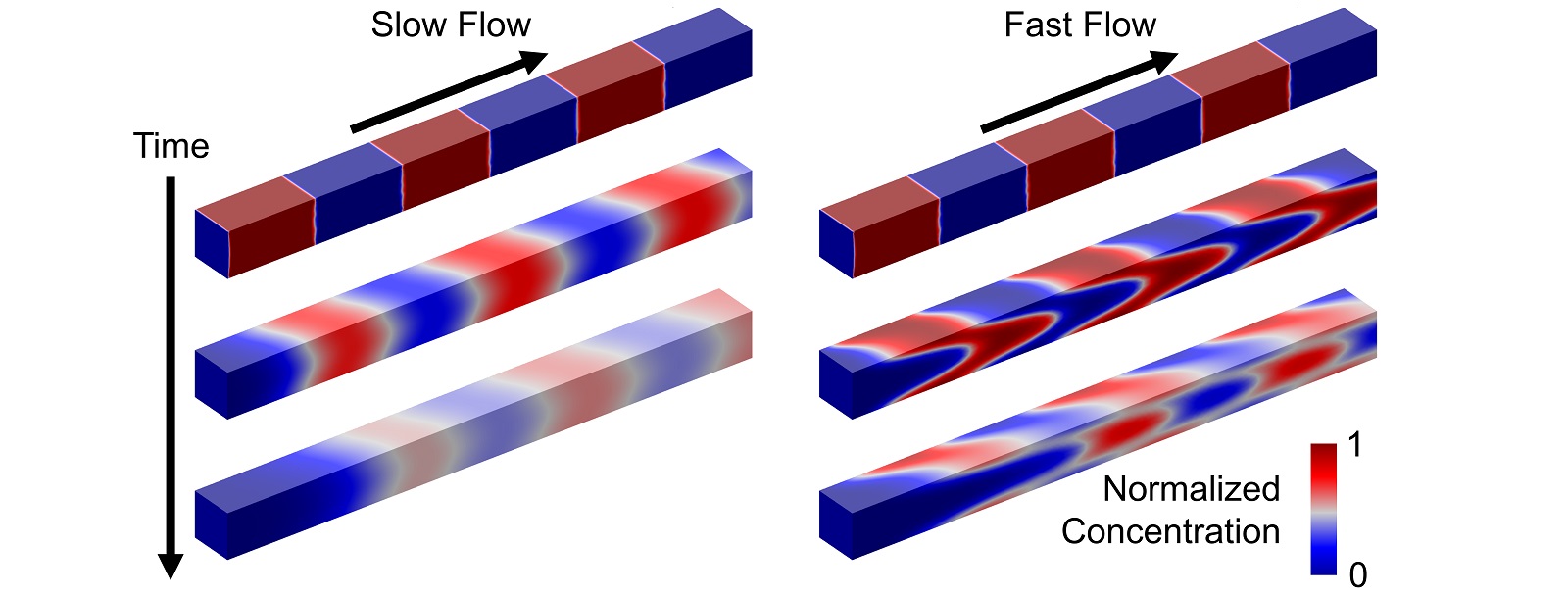
To relate the concentration gradient length to the flow and chemical parameters, we developed a COMSOL Multiphysics finite element model to simulate the flow of alternating chemical and buffer solution segments in a microchannel. Figure 1 shows how chemical concentration evolves in a stream of alternating segments of chemical and buffer solutions for slow and fast flows. The initially sharp chemical concentration gradients become longer and more diffuse over time, and grow more quickly for faster flows. Concentration gradient growth is characterized by the Peclet number, which is the ratio of transport by the flow (advection) to that by diffusion, Pe = channel height × velocity / chemical molecular diffusivity.
Slow and fast gradient growth corresponds to slow and fast flows, which in turn correspond to small and large Peclet numbers, respectively.
Because the concentrations are dilute, we used single-phase fluid flow and applied one-way coupling between the fluid mechanics and mass transport. Furthermore, higher flow rates lead to sharp concentration gradients, accounted for in our model. We also ensured that numerical diffusion is sufficiently small for these high flow rate cases.
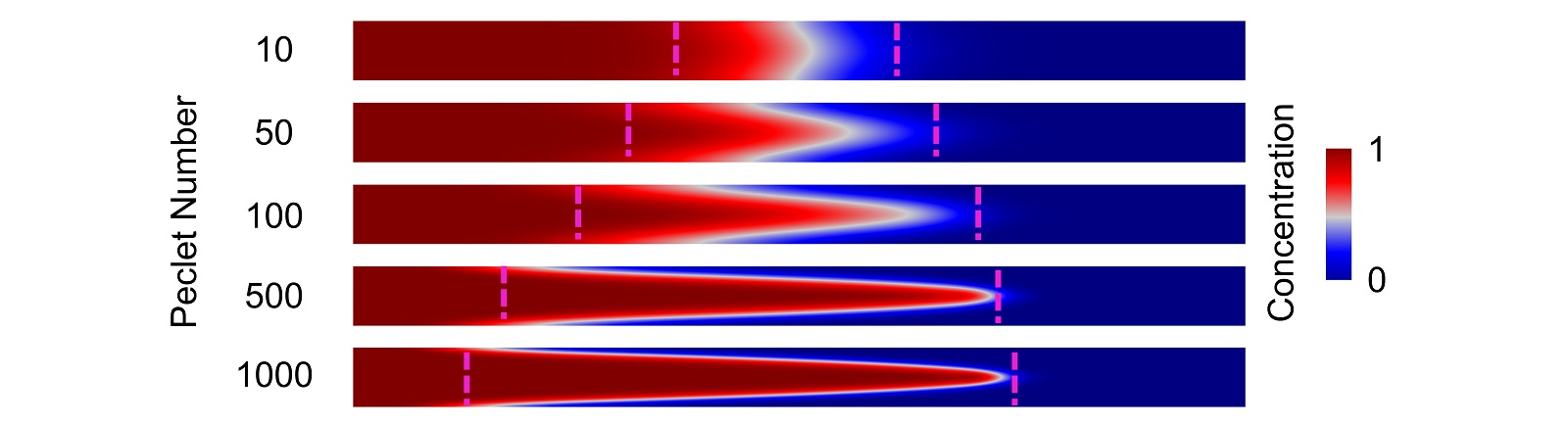
Figure 2 shows chemical concentration profiles in a vertical cross-section of a microchannel for different Peclet numbers. The Peclet number was modified here by pumping the same fluid volume (50% of the channel volume) at different speeds through the channel. The higher the flow speed (and Peclet number), the more the concentration profiles are stretched. For these simulations, the microchannel dimensions are 0.1 mm height, 1 mm width (into page), and 2 cm length and the chemical species has diffusivity 10-9 m2/s .
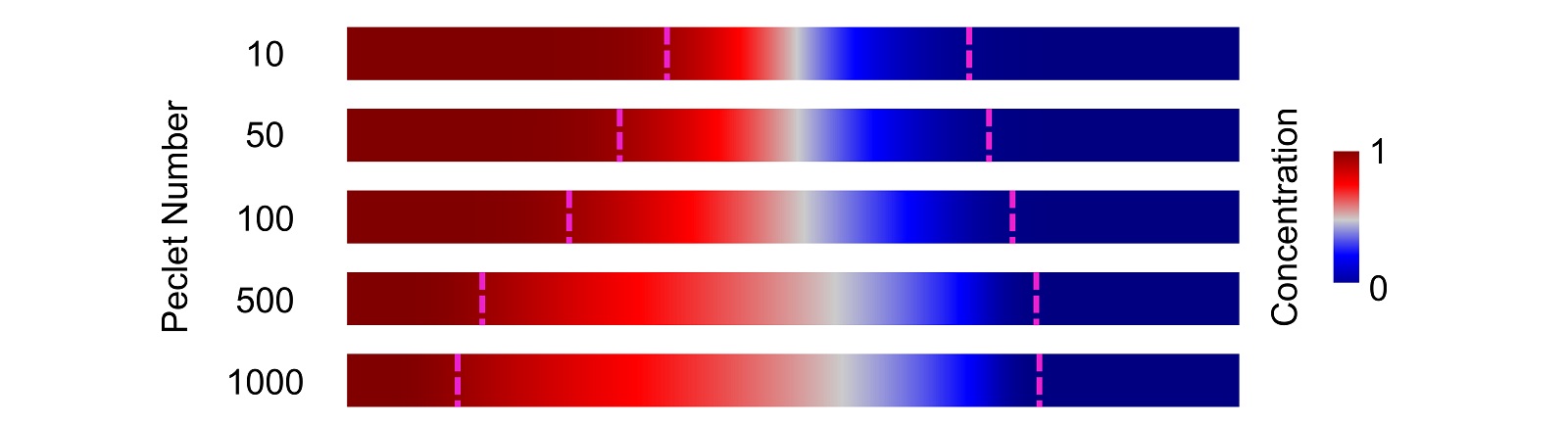
A short time after the flow stops, vertical concentration gradients equilibrate due to molecular diffusion, leaving only horizontal concentration gradients (Figure 3). The dashed magenta lines in Figures 2 and 3 indicate the 5% and 95% vertically averaged concentrations; the distance between these is the measure of gradient length.
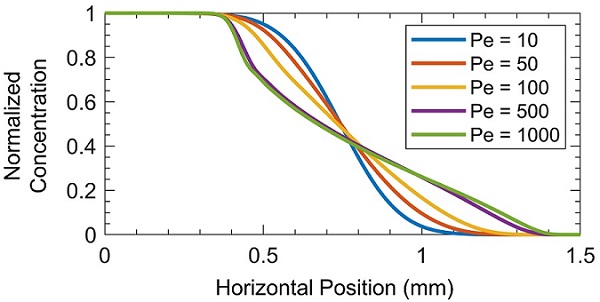
The vertically averaged concentration gradients are plotted against axial distance in Figure 4, showing how increasing the Peclet number increases the gradient length, for the same volume of pumped fluid.
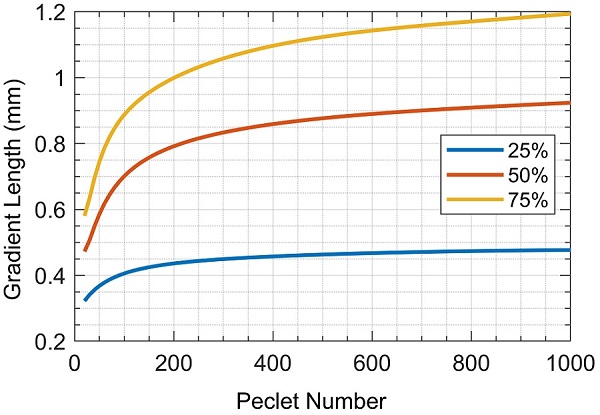
In Figure 5, the gradient length is plotted for a wide range of Peclet numbers. Each curve corresponds to the same fluid volume (as % of channel volume) pumped into the channel at different speeds. For small Peclet numbers (low flow speeds), gradient length increases sharply with increasing Peclet number. As the Peclet number increases (higher flow speeds), its effect on gradient length decreases.
For a given channel geometry, the approach presented here may be used to identify the flow speeds and pumped volumes necessary to achieve a certain gradient length, or the critical flow speed (and Peclet number) beyond which gradients would exceed a desired threshold length.
Conclusion
The length of concentration gradients in microfluidic devices depends on the flow rate, chemical molecular diffusivity, and channel geometry, and is characterized by the Peclet number, which is the ratio of transport by the flow (advection) to that by diffusion.
Finite element simulations of the fluid flow and mass transport in a microchannel enable prediction and control of concentration gradients, useful across a range of diagnostics, genomics, and pharmaceutical applications.