Technical Challenge
Artificial muscles are soft devices that mimic the motion of natural muscles and can change their shape or stiffness in response to external stimuli. Most soft artificial muscles (soft actuators) use large deformation to achieve the desired function, such as bending, contracting, extending,
twisting, snapping, etc. In addition to finite material deformation, some artificial muscles can respond to multiple external stimuli (i.e., fluid pressure, electric field, humidity, temperature, etc.), making the relationship between stimuli and response multidimensional and highly nonlinear.
Veryst Solution
Finite element-based multiphysics simulation is key to understanding the behavior of soft artificial muscles, greatly accelerating the design and material selection processes. Additionally, identifying the appropriate external stimuli (i.e., magnitude of fluid pressure, voltage amplitude, and frequency) to develop actuators with a target behavior or response is significantly faster with simulation than experimental prototyping. Simulating the response of these systems is difficult due to the coupled, non-linear physics involved in artificial muscles.
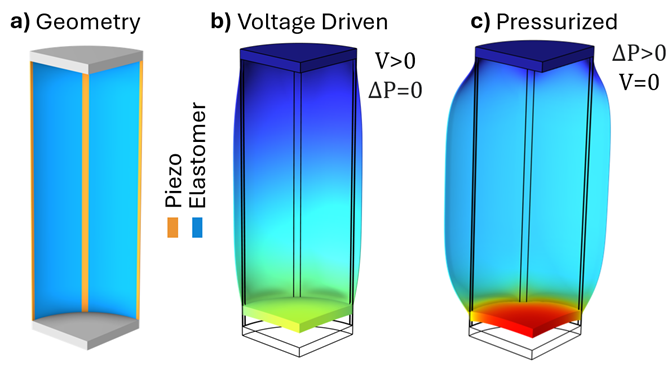
In this study, we focus on an elastomeric cylinder that encapsulates 8 piezoelectric strips (Figure 1a). The elastomeric cylinder is soft with a Young’s modulus of 10 MPa and Poisson's ratio of 0.45, whereas the piezo strips are comprised of PZT-5A, an industry standard transversely isotropic piezoelectric material, with a Young’s modulus of approximately 120 GPa MPa.
The cylindrical artificial muscle can be actuated by supplying an electric field at the piezo strips (Figure 1b), by inflating the enclosed cavity (Figure 1c), or by a combination of the two methods to achieve complex actuation behavior. The higher stiffness of the piezo strips compared to the elastomer matrix makes the muscle contract upon application of voltage or fluidic pressure. We quantify the contraction of the artificial muscle by the distance between the cylinder caps.
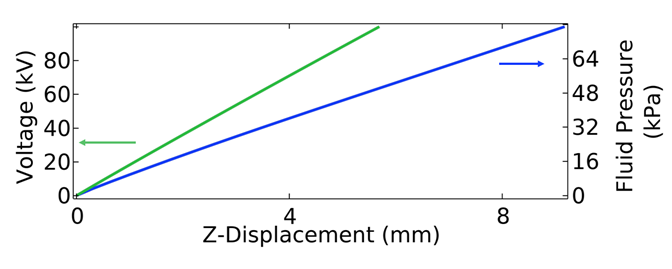
We performed finite element simulations of the actuation of the piezo artificial muscle to determine muscle contraction due to applied voltage without pressure (Figure 2, green curve) or fluid pressure without voltage (Figure 2, blue curve).
The fluidic pressure actuation method causes the cylinder to distort and deform, increasing its internal diameter. Without the significantly stiffer piezoelectric strips, the muscle would simply elongate upon inflation. However, here, the increased stiffness of the piezo strips compared to the elastomer matrix causes the muscle to contract when pressurized. The muscle contracts up to 10 mm in length using 75 kPa of pressure or 130 kV of voltage.
When instead we supply an electric field in the radial direction to the piezo strips, but no fluidic pressure, the piezo strips contract (reducing their length), causing them to bend outwards and result in a contraction of the muscle itself. In this case, 130 kV of voltage is needed for the muscle to contract by 10 mm. Figure 2 demonstrates the voltage vs displacement (green curve) and fluidic pressure vs displacement (blue curve) relationship for this artificial muscle. In both cases, the z-displacement is the response of the muscle to the input stimulus (voltage or pressure). The voltage-displacement relationship is mostly linear. However, the pressure-displacement relationship is linear at first but eventually plateaus when the elastomeric matrix is stretched beyond the limits tested here.
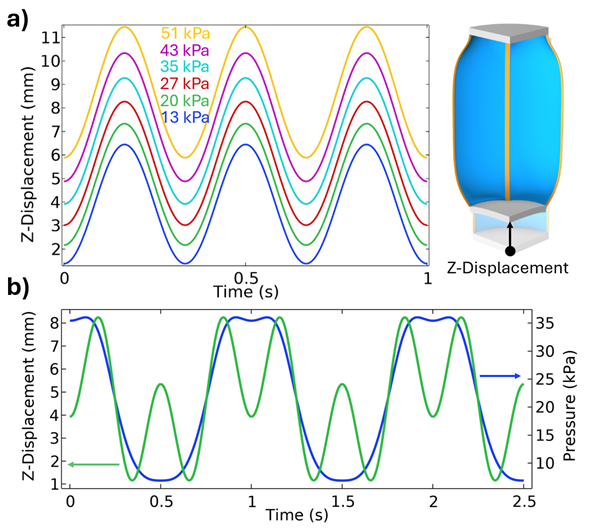
Next, we combined voltage and pressure stimuli to produce more complex responses, including alternating voltage between 0 and 100 kV at a frequency of 1/6π and fixed pressure (Figure 3a) and alternating both pressure and voltage, the former with a frequency of 1/2π and the latter with a frequency of 1/6π (Figure 3b).
The muscle’s ability to react to both stimuli (pressure and voltage) enables a wide range of possible responses and use cases. In Figure 3a we demonstrate that an initial fluid pressure can contract the muscle by 1-11 mm and that superimposing an alternating voltage can achieve precise oscillations above the desired mean.
Further, much more complex contractive displacement histories can be achieved by combining temporally varying voltage and pressure, as shown in Figure 3b.
This study demonstrates the power of multiphysics simulation to predict the response of piezoelectrically enhanced soft artificial muscles and to optimize excitation parameters such as inflation pressure, voltage amplitude, and frequency.