Technical Challenge
Microfluidic devices manipulate nanoliter fluid volumes with exquisite precision and have numerous applications in biotechnology, biopharma, and medical devices. Examples include flow cells in DNA sequencing, mRNA vaccine production in small-batch pharmaceutical processes, and lateral flow, wearable, and point-of-care diagnostic tests.
Since microfluidic devices involve small fluid volumes, they are advantageous when reagent cost is high. One of the challenges in the design of microfluidic devices is how to mix reagents rapidly in a minimal amount of space and time.
Even though microfluidic devices are compact, diffusive mixing is generally far too slow and inefficient. The efficient turbulent mixing available to larger scale systems is generally not available in microfluidic devices. Despite this, appropriate designs can achieve chaotic mixing in microfluidic devices via well-designed geometrical features such as bends, turns, and grooves. A well-designed microfluidic mixer combines two or more streams – without the excess use of reagents – in a design that can be repeatably manufactured. Understanding how mixer type and design affect mixing performance across operating regimes is essential to designing effective microfluidic mixers.
Veryst Solution
Veryst used computational fluid dynamics (CFD) simulations to compare the performance of three common microfluidic chaotic mixer designs: serpentine, ring, and herringbone. We evaluated the mixing of ethanol and water over a wide range of flow rates for each mixer design.
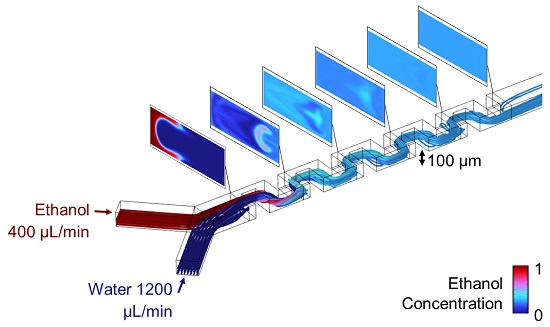
The serpentine mixer (Figure 1) contains S-shaped baffles that create a tortuous flow path. At low flow rates, the flow is purely viscous and mixing between the two fluids is dominated by molecular diffusion. Increasing the flow rate generates recirculation that enhances mixing. The recirculation is driven by inertial forces and is called “inertial secondary flow,” since it is generally weaker in magnitude compared to the main flow.
The relative strength of inertial forces and viscous forces is quantified by the dimensionless Reynolds number,
where ν is the kinematic viscosity of the mixture, Q is the total volumetric flow rate, A is the channel cross-sectional area, and Dh is the channel hydraulic diameter.
For small Reynolds numbers, viscous effects dominate and recirculation is suppressed; as the Reynolds number increases, recirculation becomes more prevalent and mixing improves.
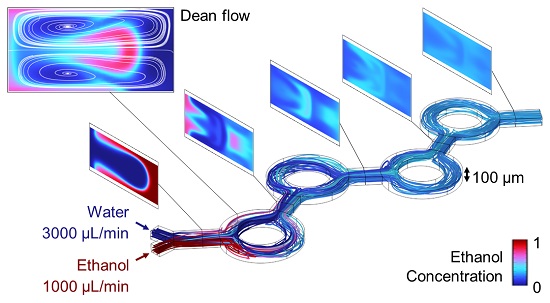
The ring mixer (Figure 2) operates by a similar principle as the serpentine mixer. The curvature of the rings exerts centrifugal forces on the fluid that, if the flow is sufficiently strong, create counter-rotating vortices in the cross-sectional plane transverse to the main flow. This special type of secondary flow is called a “Dean flow,” and the speed of the vortices is governed by the Dean number,
where R c is the radius of curvature of the channel. The flow is purely unidirectional (no vortices) for Dean numbers below 40-60, and vortical speed and mixing increase as the Dean number increases beyond that. The Dean number and mixing are increased by increasing flow rate or by decreasing the ring radius, R c .
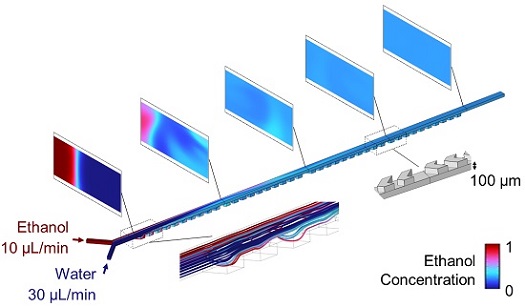
Unlike the serpentine and ring mixers, the herringbone mixer (Figure 3) does not require fluid inertia.
Herringbone mixers are designed with asymmetric grooves in the channel floor that induce flow rotation around the channel axis, much like rifling. Sets of grooves alternate in orientation to generate spatially modulated, counter-rotating fluid motion along the direction of flow. These secondary flows stretch and fold fluid elements periodically such that the distance between adjacent fluid layers halves with each cycle, a process known as the “baker’s transformation.” Hence, the distance between layers decreases exponentially with number of cycles, facilitating fast diffusive mixing across adjacent layers even in non-inertial, purely viscous flows.
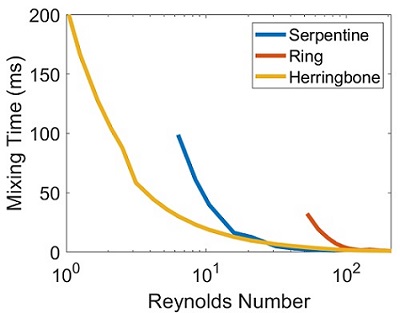
The mixing efficiency of each device is quantified by the mixing time, defined here as the time required for the coefficient of variation of the ethanol mass fraction to be cut in half. The coefficient of variation is the ratio between the standard deviation and the mean of the ethanol mass fraction in the channel cross section.
Figure 4 plots the mixing time for each device as a function of the Reynolds number. The serpentine and ring mixers demonstrate efficient mixing only at Reynolds numbers greater than 10 and 100, respectively. By contrast, the herringbone mixer exhibits short mixing times (less than 200 milliseconds) for Reynolds numbers as low as 1. This result implies that the herringbone mixer can operate across a much wider range of flow rates.
Conclusion
Veryst evaluated the mixing performance of three prototypical microfluidic mixers using COMSOL Multiphysics. Our simulations showed that the herringbone mixer exhibits superior mixing performance over a larger operating window compared to the serpentine and ring mixers.
Simulations such as these can be used to design effective microfluidic mixers to optimize performance in microfluidic devices, thereby reducing the number of required experimental prototypes and increasing the value of each.